08. PyTorch 论文复现¶
欢迎来到第二阶段项目:PyTorch 论文复现!
在这个项目中,我们将复现一篇机器学习研究论文,并使用 PyTorch 从头开始创建一个视觉变换器(Vision Transformer,ViT)。
随后,我们将看到这种先进的计算机视觉架构 ViT 在 FoodVision Mini 问题上的表现。
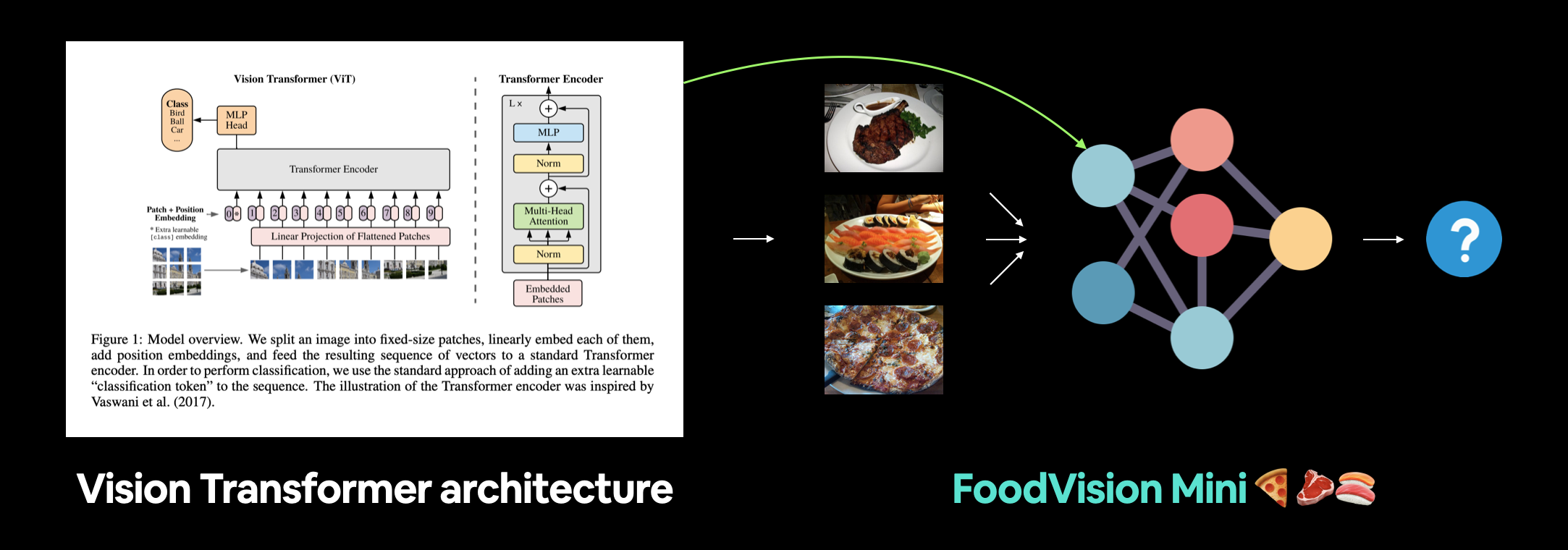
在第二阶段项目中,我们将专注于重建视觉变换器(ViT)计算机视觉架构,并将其应用于 FoodVision Mini 问题,以对不同披萨、牛排和寿司的图像进行分类。
什么是机器学习研究论文?¶
机器学习研究论文是一篇科学论文,详细介绍了研究团队在特定领域的研究成果。
机器学习研究论文的内容可能因论文而异,但它们通常遵循以下结构:
| 部分 | 内容 |
|---|---|
| 摘要 | 论文主要发现/贡献的概述/总结。 |
| 引言 | 论文的主要问题及以往用于尝试解决该问题的方法细节。 |
| 方法 | 研究人员是如何进行研究的?例如,使用了哪些模型、数据源、训练设置? |
| 结果 | 论文的成果是什么?如果使用了新类型的模型或训练设置,其结果与以往研究相比如何?(这里实验跟踪非常有用) |
| 结论 | 所提出方法的局限性是什么?研究社区的下一步是什么? |
| 参考文献 | 研究人员参考了哪些资源/其他论文来构建自己的研究成果? |
| 附录 | 是否有未包含在上述任何部分中的额外资源/发现? |
为什么要复现机器学习研究论文?¶
一篇机器学习研究论文通常是世界上最优秀的机器学习团队数月工作和实验的浓缩,这些内容被精简成几页文字。
如果这些实验在你所研究的问题相关领域取得了更好的结果,那么去检验一下它们是很有意义的。
此外,复现他人的工作是锻炼你技能的绝佳方式。

乔治·霍茨是comma.ai的创始人,这是一家自动驾驶汽车公司,他在Twitch上直播机器学习编程,这些视频完整地发布在YouTube上。我从他的一次直播中摘录了这句话。"٭"表示机器学习工程通常涉及额外的步骤,如数据预处理和使你的模型可供他人使用(部署)。
当你刚开始尝试复现研究论文时,你很可能会感到不知所措。
这是正常的。
研究团队花费数周、数月甚至数年时间来创造这些成果,所以如果你需要一些时间来阅读甚至重现这些工作,这是可以理解的。
复现研究是一个如此艰巨的问题,以至于诞生了一些卓越的机器学习库和工具,如HuggingFace、PyTorch Image Models(timm库)和fast.ai,它们致力于使机器学习研究更加易于访问。
在哪里可以找到机器学习研究论文的代码示例?¶
当你开始接触机器学习研究时,首先会注意到的是:这方面的研究非常多。
所以要注意,试图跟上这一切就像是试图跑赢仓鼠轮一样。
跟随你的兴趣,挑选一些对你来说突出的内容。
这样说来,有几个地方可以找到并阅读机器学习研究论文(及其代码):
| 资源 | 是什么? |
|---|---|
| arXiv | 发音为 "archive",arXiv 是一个免费且开放的资源,用于阅读从物理学到计算机科学(包括机器学习)的各种技术文章。 |
| AK Twitter | AK Twitter 账号发布机器学习研究亮点,几乎每天都有实时演示。我不理解 9/10 的帖子,但我发现偶尔探索一下很有趣。 |
| Papers with Code | 一个精选的机器学习论文集合,其中许多论文附有代码资源。还包括一系列常见的机器学习数据集、基准和当前最先进的模型。 |
lucidrains 的 vit-pytorch GitHub 仓库 |
与其说是一个寻找研究论文的地方,不如说是一个大规模、特定焦点下用代码复现论文的示例。vit-pytorch 仓库是一个收集了来自各种研究论文的 Vision Transformer 模型架构,用 PyTorch 代码复现的集合(本笔记本的许多灵感来自于此仓库)。 |
注意: 这个列表远非详尽。我只列出了几个地方,是我个人最常使用的。所以要注意偏见。然而,我发现即使是这个简短的列表,也常常能满足我对领域内动态的了解需求。再多一些,我可能会发疯。
我们将要涵盖的内容¶
与其讨论如何复制一篇论文,我们不如亲自动手,真正地复制一篇论文。
复制所有论文的过程会有所不同,但通过体验一次复制的过程,我们将获得继续复制的动力。
更具体地说,我们将复制机器学习研究论文An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale(ViT论文),使用PyTorch实现。
Transformer神经网络架构最初在机器学习研究论文Attention is all you need中被介绍。
而最初的Transformer架构被设计用于处理一维(1D)的文本序列。
Transformer架构通常被认为是任何使用注意力机制)作为其主要学习层的神经网络。类似于卷积神经网络(CNN)使用卷积作为其主要学习层。
正如名称所示,Vision Transformer(ViT)架构旨在将原始Transformer架构适应于视觉问题(分类是第一个,此后许多其他问题也随之而来)。
最初的Vision Transformer在过去几年中经历了几次迭代,然而,我们将专注于复制最初的版本,也称为“原始Vision Transformer”。因为如果你能重现原始版本,你就能适应其他版本。
我们将专注于按照原始ViT论文构建ViT架构,并将其应用于FoodVision Mini。
| 主题 | 内容 |
|---|---|
| 0. 环境设置 | 我们在过去的几个部分中编写了不少有用的代码,让我们下载它并确保我们可以再次使用它。 |
| 1. 获取数据 | 让我们获取我们一直在使用的披萨、牛排和寿司图像分类数据集,并构建一个Vision Transformer来尝试改进FoodVision Mini模型的结果。 |
| 2. 创建数据集和数据加载器 | 我们将使用在第05章节中编写的data_setup.py脚本,设置我们的数据加载器。 |
| 3. 复制ViT论文:概述 | 复制机器学习研究论文可能是一个相当大的挑战,所以在我们开始之前,让我们将ViT论文分解成更小的部分,这样我们可以逐部分复制论文。 |
| 4. 公式1:Patch Embedding | ViT架构由四个主要公式组成,第一个是patch和位置嵌入。或者将图像转换为一系列可学习的patch。 |
| 5. 公式2:多头注意力(MSA) | 自注意力/多头自注意力(MSA)机制是每个Transformer架构的核心,包括ViT架构,让我们使用PyTorch的内置层创建一个MSA块。 |
| 6. 公式3:多层感知器(MLP) | ViT架构使用多层感知器作为其Transformer编码器的一部分及其输出层。让我们首先为Transformer编码器创建一个MLP。 |
| 7. 创建Transformer编码器 | Transformer编码器通常由MSA(公式2)和MLP(公式3)交替层组成,通过残差连接连接在一起。让我们通过将第5节和第6节中创建的层堆叠在一起来创建一个。 |
| 8. 将所有部分组合起来创建ViT | 我们已经有了创建ViT架构的所有拼图,让我们将它们全部组合到一个类中,我们可以调用它作为我们的模型。 |
| 9. 为我们的ViT模型设置训练代码 | 训练我们的自定义ViT实现类似于我们之前训练的所有其他模型。并且由于我们在engine.py中的train()函数,我们可以用几行代码开始训练。 |
10. 使用torchvision.models中的预训练ViT |
训练像ViT这样的大型模型通常需要大量的数据。由于我们只处理少量的披萨、牛排和寿司图像,让我们看看是否可以利用迁移学习的力量来提高我们的性能。 |
| 11. 对自定义图像进行预测 | 机器学习的神奇之处在于看到它在您自己的数据上工作,所以让我们采用表现最好的模型,并在臭名昭著的pizza-dad图像(一张我爸爸吃披萨的照片)上测试FoodVision Mini。 |
注意: 尽管我们将专注于复制ViT论文,但要避免过于沉迷于某一篇论文,因为更好的方法往往会很快出现,所以技能应该是保持好奇心,同时建立将数学和页面上的文字转化为工作代码的基本技能。
术语¶
在本笔记本中将会出现相当多的缩写词。
鉴于此,以下是一些定义:
- ViT - 代表 Vision Transformer(我们将主要关注复制的神经网络架构)。
- ViT 论文 - 指介绍 ViT 架构的原始机器学习研究论文的简称,即 An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale。每当提到 ViT 论文 时,您可以确信它指的是这篇论文。
如何获取帮助?¶
本课程的所有资料都可以在 GitHub 上找到。
如果你遇到问题,可以在课程的 GitHub Discussions 页面提问。
当然,还有 PyTorch 文档和 PyTorch 开发者论坛,这是所有 PyTorch 相关问题的非常有帮助的地方。
0. 环境设置¶
与之前一样,让我们确保已经安装了本节所需的所有模块。
我们将导入在 05. PyTorch 模块化 中创建的 Python 脚本(如 data_setup.py 和 engine.py)。
为此,我们将从 pytorch-deep-learning 仓库下载 going_modular 目录(如果尚未下载的话)。
我们还将获取 torchinfo 包(如果尚未安装)。
torchinfo 将在后续帮助我们直观地展示模型结构。
并且由于稍后我们将使用 torchvision v0.13 版本(自 2022 年 7 月起可用),我们将确保已安装最新版本。
# For this notebook to run with updated APIs, we need torch 1.12+ and torchvision 0.13+
try:
import torch
import torchvision
assert int(torch.__version__.split(".")[1]) >= 12 or int(torch.__version__.split(".")[0]) == 2, "torch version should be 1.12+"
assert int(torchvision.__version__.split(".")[1]) >= 13, "torchvision version should be 0.13+"
print(f"torch version: {torch.__version__}")
print(f"torchvision version: {torchvision.__version__}")
except:
print(f"[INFO] torch/torchvision versions not as required, installing nightly versions.")
!pip3 install -U torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cu118
import torch
import torchvision
print(f"torch version: {torch.__version__}")
print(f"torchvision version: {torchvision.__version__}")
torch version: 2.1.0+cu118 torchvision version: 0.16.0+cu118
注意: 如果你使用的是 Google Colab,并且上面的单元格开始安装各种软件包,你可能需要在运行上述单元格后重启运行时。重启后,你可以再次运行该单元格,并验证你已经安装了正确版本的
torch和torchvision。
接下来,我们将继续进行常规导入,设置设备无关代码,这次我们还将从 GitHub 获取 helper_functions.py 脚本。
helper_functions.py 脚本包含我们在前几节中创建的几个函数:
set_seeds()用于设置随机种子(在 07. PyTorch 实验跟踪部分 0 中创建)。download_data()用于根据链接下载数据源(在 07. PyTorch 实验跟踪部分 1 中创建)。plot_loss_curves()用于检查我们模型的训练结果(在 04. PyTorch 自定义数据集部分 7.8 中创建)。
注意: 将
helper_functions.py脚本中的许多函数合并到going_modular/going_modular/utils.py中可能是一个更好的主意,也许这是你想尝试的扩展。
# Continue with regular imports
import matplotlib.pyplot as plt
import torch
import torchvision
from torch import nn
from torchvision import transforms
# Try to get torchinfo, install it if it doesn't work
try:
from torchinfo import summary
except:
print("[INFO] Couldn't find torchinfo... installing it.")
!pip install -q torchinfo
from torchinfo import summary
# Try to import the going_modular directory, download it from GitHub if it doesn't work
try:
from going_modular.going_modular import data_setup, engine
from helper_functions import download_data, set_seeds, plot_loss_curves
except:
# Get the going_modular scripts
print("[INFO] Couldn't find going_modular or helper_functions scripts... downloading them from GitHub.")
!git clone https://github.com/mrdbourke/pytorch-deep-learning
!mv pytorch-deep-learning/going_modular .
!mv pytorch-deep-learning/helper_functions.py . # get the helper_functions.py script
!rm -rf pytorch-deep-learning
from going_modular.going_modular import data_setup, engine
from helper_functions import download_data, set_seeds, plot_loss_curves
[INFO] Couldn't find torchinfo... installing it. [INFO] Couldn't find going_modular or helper_functions scripts... downloading them from GitHub. Cloning into 'pytorch-deep-learning'... remote: Enumerating objects: 4033, done. remote: Counting objects: 100% (1224/1224), done. remote: Compressing objects: 100% (225/225), done. remote: Total 4033 (delta 1067), reused 1097 (delta 996), pack-reused 2809 Receiving objects: 100% (4033/4033), 649.59 MiB | 34.16 MiB/s, done. Resolving deltas: 100% (2358/2358), done. Updating files: 100% (248/248), done.
注意: 如果你正在使用 Google Colab,并且还没有启用 GPU,现在是时候通过
Runtime -> Change runtime type -> Hardware accelerator -> GPU来启用一个 GPU 了。
device = "cuda" if torch.cuda.is_available() else "cpu"
device
'cuda'
1. 获取数据¶
由于我们继续使用 FoodVision Mini,让我们下载我们一直在使用的披萨、牛排和寿司图像数据集。
为此,我们可以使用我们在07. PyTorch 实验跟踪部分 1中创建的 helper_functions.py 中的 download_data() 函数。
我们将 source 设置为 pizza_steak_sushi.zip 数据的原始 GitHub 链接,并将 destination 设置为 pizza_steak_sushi。
# Download pizza, steak, sushi images from GitHub
image_path = download_data(source="https://github.com/mrdbourke/pytorch-deep-learning/raw/main/data/pizza_steak_sushi.zip",
destination="pizza_steak_sushi")
image_path
[INFO] data/pizza_steak_sushi directory exists, skipping download.
PosixPath('data/pizza_steak_sushi')
太棒了!数据已下载,接下来我们设置训练和测试目录。
# Setup directory paths to train and test images
train_dir = image_path / "train"
test_dir = image_path / "test"
2. 创建数据集和数据加载器¶
现在我们有了一些数据,接下来将其转换为 DataLoader。
为此,我们可以使用 data_setup.py 中的 create_dataloaders() 函数。
首先,我们将创建一个转换来准备我们的图像。
这是第一个参考 ViT 论文的地方。
在表 3 中,训练分辨率被提及为 224(高度=224,宽度=224)。
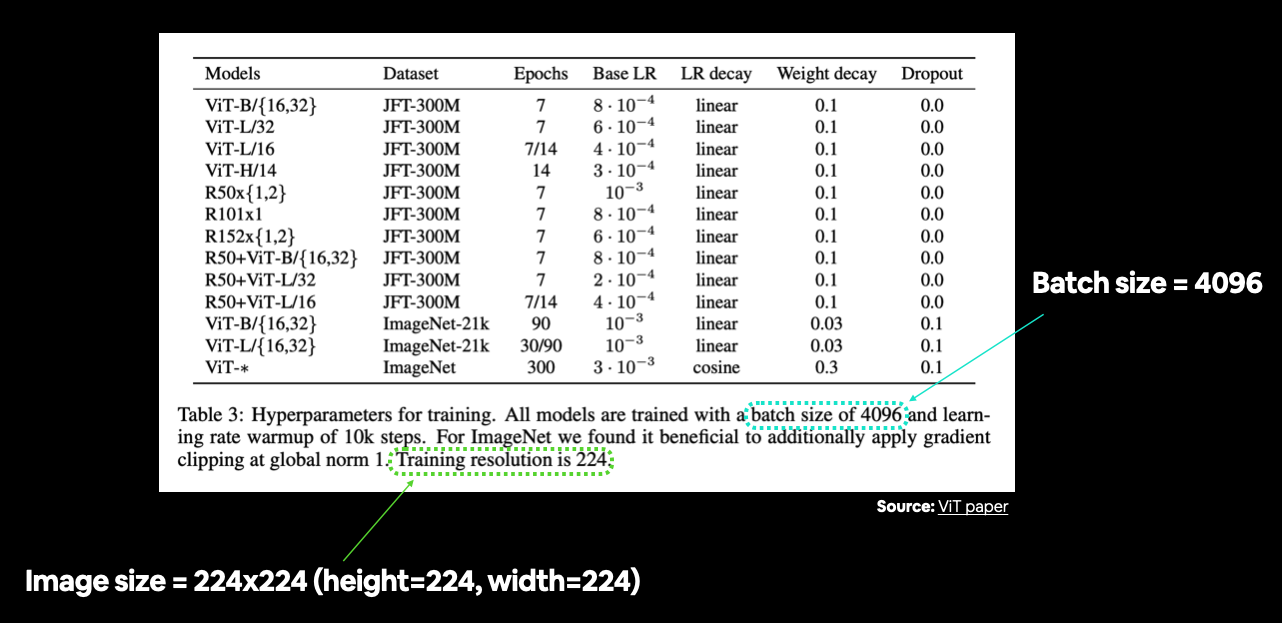
你通常可以在表格中找到各种超参数设置。在这种情况下,我们仍在准备数据,因此我们主要关注图像大小和批次大小等事项。来源:ViT 论文中的表 3。
因此,我们将确保我们的转换适当地调整图像大小。
并且由于我们将从头开始训练我们的模型(一开始不进行迁移学习),我们不会像在 06. PyTorch 迁移学习 第 2.1 节 中那样提供 normalize 转换。
2.1 准备图像转换¶
# Create image size (from Table 3 in the ViT paper)
IMG_SIZE = 224
# Create transform pipeline manually
manual_transforms = transforms.Compose([
transforms.Resize((IMG_SIZE, IMG_SIZE)),
transforms.ToTensor(),
])
print(f"Manually created transforms: {manual_transforms}")
Manually created transforms: Compose(
Resize(size=(224, 224), interpolation=bilinear, max_size=None, antialias=None)
ToTensor()
)
2.2 将图像转换为 DataLoader¶
变换已创建!
现在让我们创建我们的 DataLoader。
ViT 论文中提到使用 4096 的批次大小,这是我们一直在使用的批次大小(32)的 128 倍。
然而,我们将坚持使用 32 的批次大小。
为什么?
因为一些硬件(包括 Google Colab 的免费层级)可能无法处理 4096 的批次大小。
使用 4096 的批次大小意味着一次需要将 4096 张图像放入 GPU 内存中。
当你拥有能够处理这种情况的硬件时,比如谷歌的研究团队经常做的那样,这是可行的,但当你在一台 GPU 上运行时(比如使用 Google Colab),确保在小批次大小下先让事情运行起来是个好主意。
这个项目的一个扩展可能是尝试更高的批次大小值,看看会发生什么。
注意: 我们在
create_dataloaders()函数中使用pin_memory=True参数来加速计算。pin_memory=True通过“固定”之前见过的示例,避免了 CPU 和 GPU 内存之间不必要的内存复制。尽管这种好处可能在更大的数据集大小下才能看到(我们的 FoodVision Mini 数据集相当小)。然而,设置pin_memory=True并不总是能提高性能(这是机器学习中那些有时有效有时无效的情况之一),所以最好是实验、实验、再实验。更多信息请参见 PyTorch 的torch.utils.data.DataLoader文档 或 Horace He 的 Making Deep Learning Go Brrrr from First Principles。
# Set the batch size
BATCH_SIZE = 32 # this is lower than the ViT paper but it's because we're starting small
# Create data loaders
train_dataloader, test_dataloader, class_names = data_setup.create_dataloaders(
train_dir=train_dir,
test_dir=test_dir,
transform=manual_transforms, # use manually created transforms
batch_size=BATCH_SIZE
)
train_dataloader, test_dataloader, class_names
(<torch.utils.data.dataloader.DataLoader at 0x7f18845ff0d0>, <torch.utils.data.dataloader.DataLoader at 0x7f17f3f5f520>, ['pizza', 'steak', 'sushi'])
# Get a batch of images
image_batch, label_batch = next(iter(train_dataloader))
# Get a single image from the batch
image, label = image_batch[0], label_batch[0]
# View the batch shapes
image.shape, label
(torch.Size([3, 224, 224]), tensor(2))
太棒了!
现在让我们用 matplotlib 绘制图像及其标签。
# Plot image with matplotlib
plt.imshow(image.permute(1, 2, 0)) # rearrange image dimensions to suit matplotlib [color_channels, height, width] -> [height, width, color_channels]
plt.title(class_names[label])
plt.axis(False);
太好了!
看来我们的图片导入没有问题,接下来我们继续进行论文复现工作。
3. 复现 ViT 论文:概述¶
在我们编写更多代码之前,让我们先讨论一下我们要做什么。
我们希望为我们的问题——FoodVision Mini,复现 ViT 论文。
因此,我们的模型输入是:披萨、牛排和寿司的图像。
而我们理想的模型输出是:预测的标签,即披萨、牛排或寿司。
这与我们在前几节中所做的没有什么不同。
问题是:我们如何从输入到期望的输出?
3.1 输入与输出,层与块¶
ViT 是一种深度学习神经网络架构。
任何神经网络架构通常都由 层 组成。
一组层通常被称为一个 块。
将许多块堆叠在一起就构成了整个架构。
一个 层 接受输入(比如一个图像张量),对其执行某种操作(例如层中的 forward() 方法所定义的操作),然后返回输出。
因此,如果一个 单层 接受输入并产生输出,那么一组层或一个 块 同样接受输入并产生输出。
让我们具体化这一点:
- 层 - 接受输入,对其执行某种操作,返回输出。
- 块 - 一组层,接受输入,对其执行一系列操作,返回输出。
- 架构(或模型) - 一组块,接受输入,对其执行一系列操作,返回输出。
这种理念正是我们将用来复现 ViT 论文的方法。
我们将逐层、逐块、逐函数地构建,像拼乐高一样将拼图的碎片组合起来,以获得我们期望的整体架构。
我们这样做的原因是,阅读整篇研究论文可能会令人望而生畏。
因此,为了更好地理解,我们将从单层的输入和输出开始,逐步上升到整个模型的输入和输出。
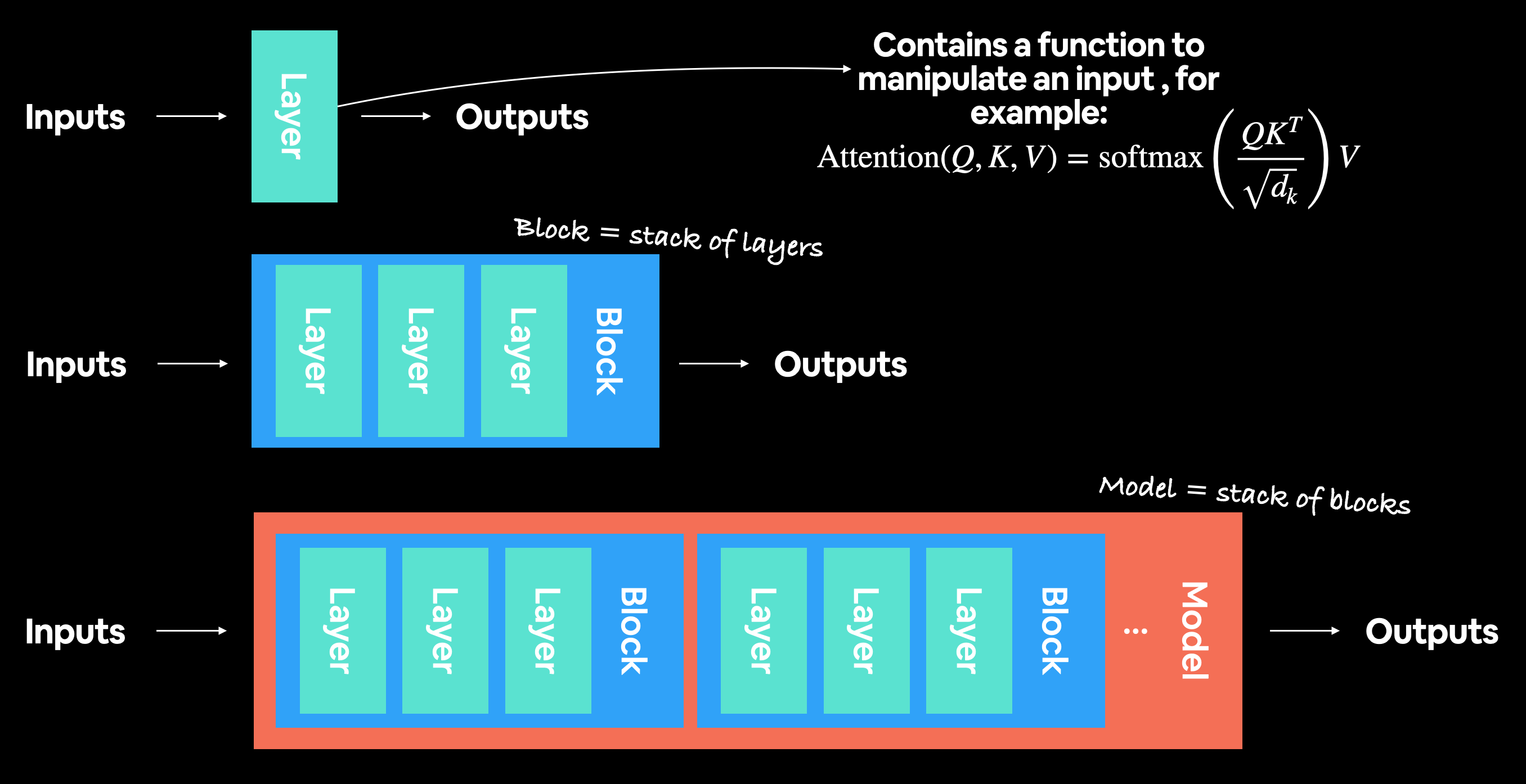
现代深度学习架构通常是一组层和块。层接受输入(数据以数值形式表示),通过某种操作(例如上图所示的自注意力公式,然而,这个操作可以是几乎任何形式)对其进行处理,然后输出。块通常是堆叠在一起的层,对单层进行类似的操作,但执行多次。
3.2 深入解析:ViT的构成是什么?¶
关于ViT模型的细节在论文中随处可见。
找到所有这些细节就像是一场大型的寻宝游戏!
记住,一篇研究论文通常是数月工作的浓缩,因此需要一些练习才能复制其中的内容,这是可以理解的。
然而,我们将主要参考以下三个资源来了解架构设计:
- 图1 - 这从图形角度概述了模型,你几乎可以仅凭这张图来重建架构。
- 第3.1节中的四个方程 - 这些方程为图1中的彩色块提供了更多的数学基础。
- 表1 - 该表展示了不同ViT模型变体的各种超参数设置(如层数和隐藏单元数)。我们将重点关注最小版本,即ViT-Base。
3.2.1 探索图1¶
让我们从ViT论文的图1开始。
我们主要关注的是:
- 层 - 接受一个输入,对输入执行操作或函数,产生一个输出。
- 块 - 由多个层组成的集合,同样接受一个输入并产生一个输出。
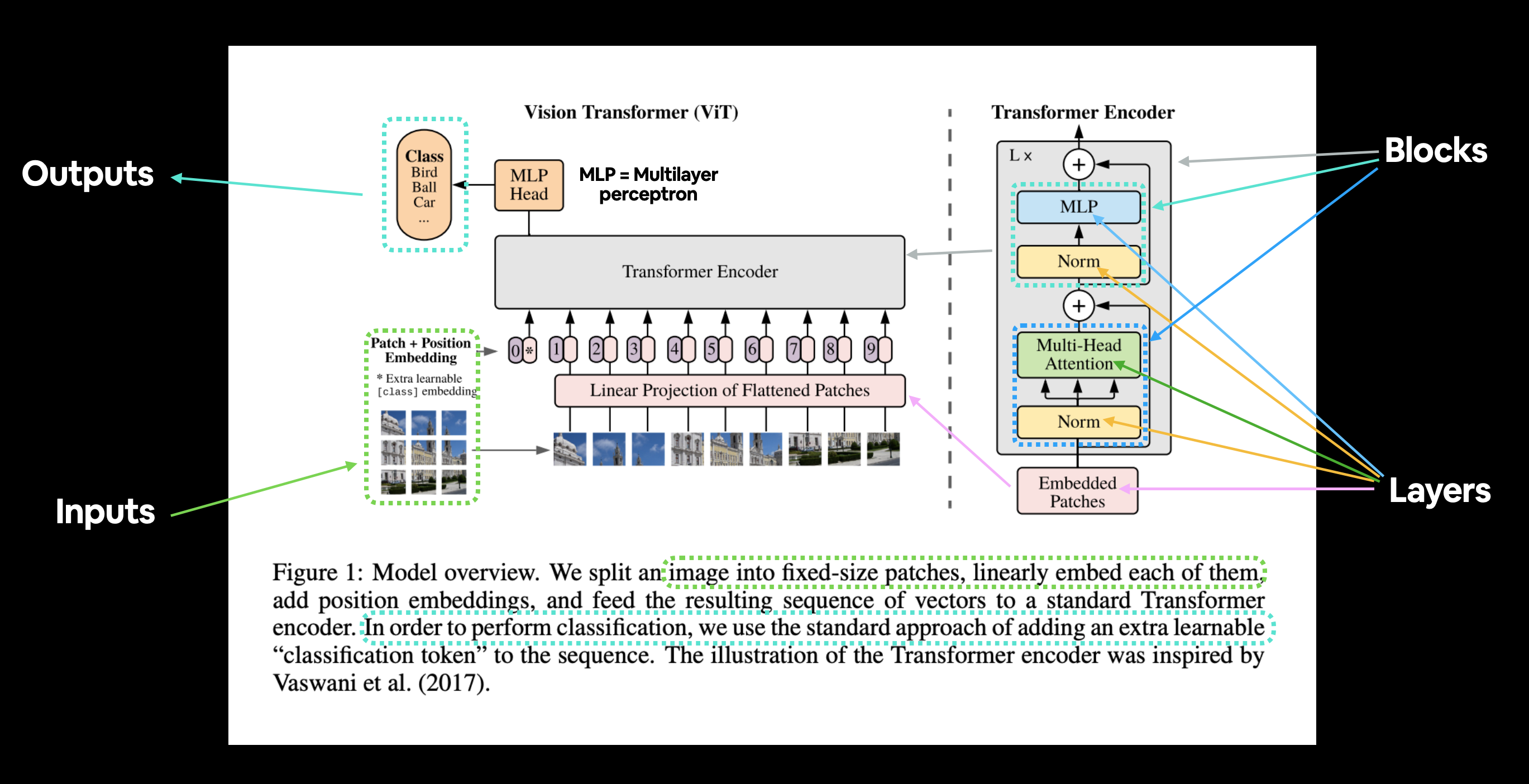
图1来自ViT论文,展示了构成架构的不同输入、输出、层和块。我们的目标是使用PyTorch代码复制这些内容。
ViT架构包含几个阶段:
- 分块 + 位置嵌入(输入) - 将输入图像转换为图像块序列,并添加位置编号以指定图像块的顺序。
- 扁平化分块的线性投影(嵌入分块) - 图像块被转换为嵌入,使用嵌入而不是图像值的好处是嵌入是一种可学习的表示(通常以向量形式),可以随着训练而改进。
- 归一化 - 这是指“层归一化”或“LayerNorm”,是一种用于正则化(减少过拟合)神经网络的技术,可以通过PyTorch层
torch.nn.LayerNorm()使用。 - 多头注意力 - 这是一个多头自注意力层,简称“MSA”。可以通过PyTorch层
torch.nn.MultiheadAttention()创建MSA层。 - MLP(或多层感知机) - MLP通常指的是任何前馈层的集合(或在PyTorch的情况下,具有
forward()方法的层的集合)。在ViT论文中,作者将MLP称为“MLP块”,它包含两个torch.nn.Linear()层,中间有一个torch.nn.GELU()非线性激活函数(第3.1节),每个层后面都有一个torch.nn.Dropout()层(附录B.1)。 - Transformer编码器 - Transformer编码器是上述层的集合。Transformer编码器内部有两个跳跃连接(“+”符号),意味着层的输入不仅直接传递到后续层,还传递到紧邻的层。整个ViT架构由多个堆叠在一起的Transformer编码器组成。
- MLP头 - 这是架构的输出层,它将输入的学习特征转换为类别输出。由于我们正在进行图像分类,你也可以称其为“分类器头”。MLP头的结构类似于MLP块。
你可能会注意到,ViT架构的许多部分都可以用现有的PyTorch层创建。
这是因为PyTorch的设计目的之一就是为研究人员和机器学习从业者创建可重用的神经网络层。
问题: 为什么不从头开始编写所有代码?
你当然可以通过用自定义的PyTorch层重现论文中的所有数学方程来实现这一点,这肯定是一个有教育意义的练习,然而,使用现有的PyTorch层通常更受欢迎,因为现有的层通常经过广泛测试和性能检查,以确保它们正确且快速运行。
注意: 我们将专注于编写PyTorch代码来创建这些层。关于每个层的功能背景,我建议阅读完整的ViT论文或阅读每个层的链接资源。
让我们将图1改编为我们的FoodVision Mini问题,即将食物图像分类为披萨、牛排或寿司。
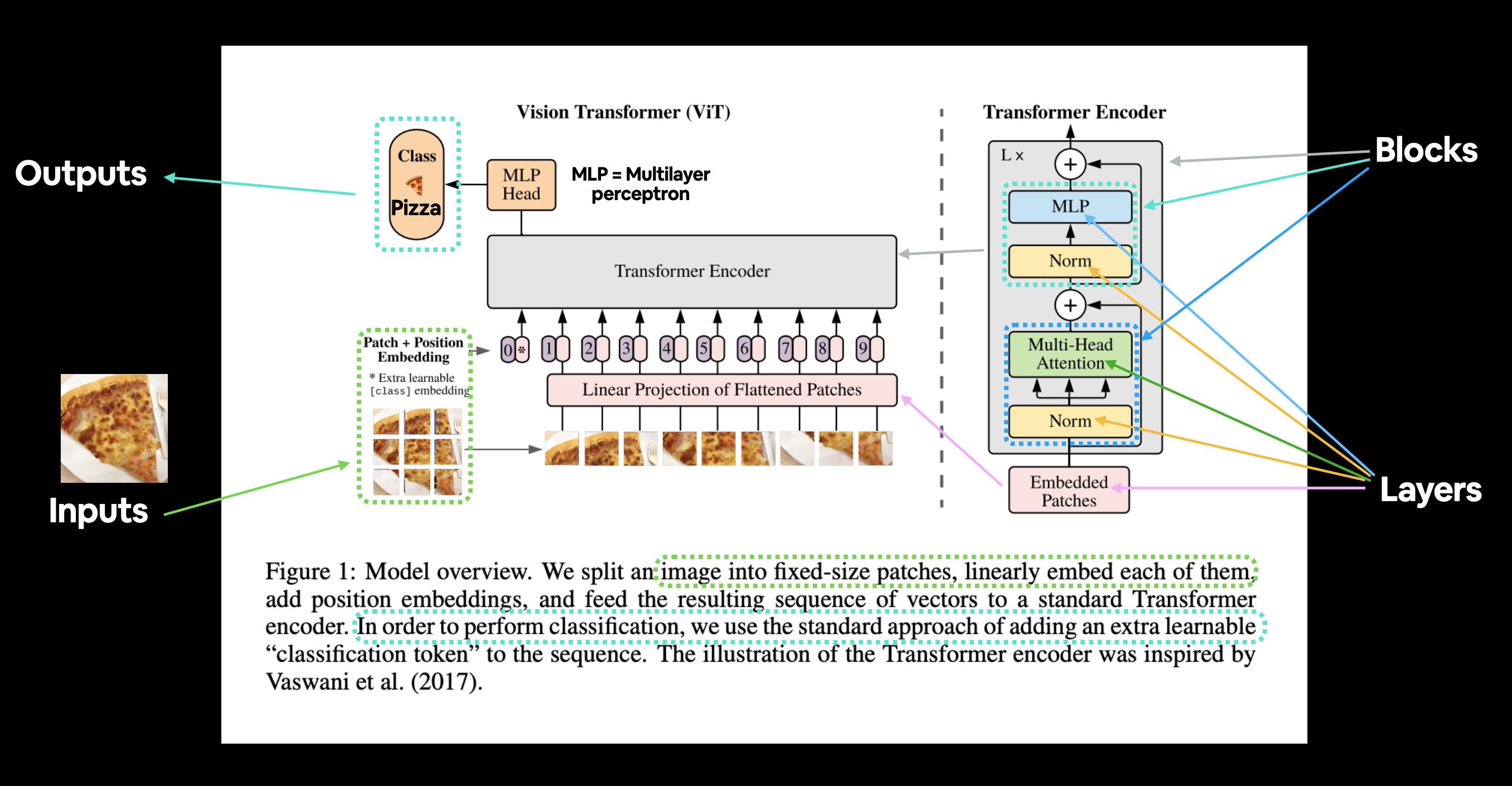
图1来自ViT论文改编为FoodVision Mini。食物图像进入(披萨),图像被转换为分块,然后投影到嵌入中。嵌入然后通过各个层和块,并(希望)返回类别“披萨”。
3.2.2 探索四个方程¶
接下来我们要重点研究的是ViT论文中的四个方程,它们位于第3.1节。
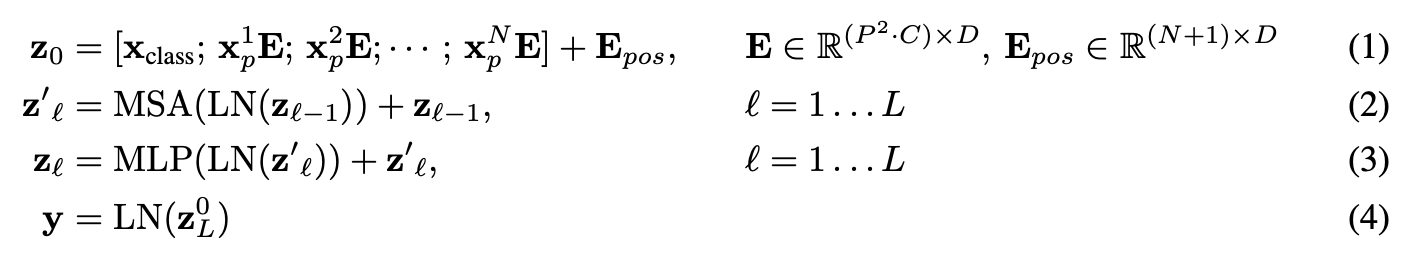
这四个方程代表了ViT架构中四个主要部分的数学原理。
第3.1节描述了每个方程(为了简洁,省略了一些文本,加粗的文本是我添加的):
| 方程编号 | ViT论文第3.1节的描述 |
|---|---|
| 1 | ...Transformer在整个层中使用恒定的潜在向量大小$D$,因此我们将图像块展平并通过可训练的线性投影映射到$D$维(方程1)。我们将这个投影的输出称为图像块嵌入...位置嵌入被添加到图像块嵌入中以保留位置信息。我们使用标准的可学习的1D位置嵌入... |
| 2 | Transformer编码器(Vaswani等人,2017)由多头自注意力(MSA,见附录A)和MLP块交替层组成(方程2, 3)。在每个块之前应用层归一化(LN),并且在每个块之后应用残差连接(Wang等人,2019;Baevski & Auli,2019)。 |
| 3 | 与方程2相同。 |
| 4 | 类似于BERT的[class]令牌,我们在嵌入的图像块序列前添加一个可学习的嵌入 $\left(\mathbf{z}_{0}^{0}=\mathbf{x}_{\text {class }}\right)$,其在Transformer编码器输出处的状态 $\left(\mathbf{z}_{L}^{0}\right)$ 作为图像表示 $\mathbf{y}$(方程4)... |
让我们将这些描述映射到图1中的ViT架构。
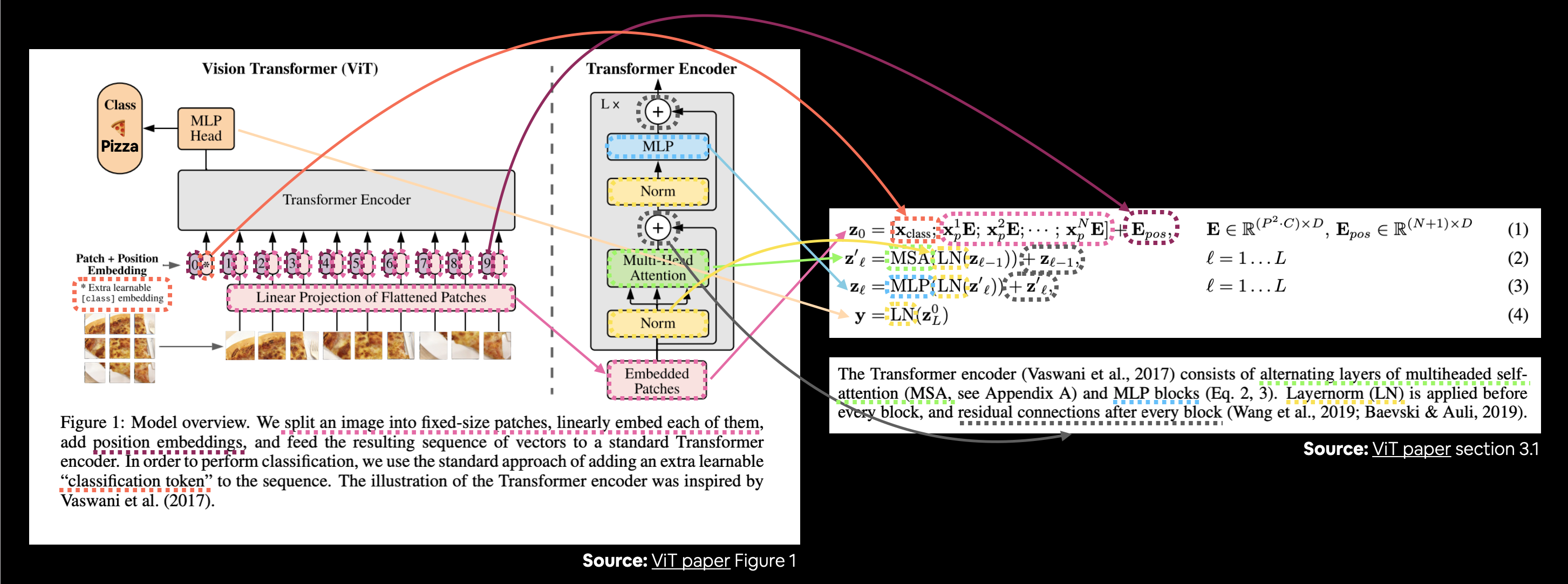
将ViT论文的图1与第3.1节中描述每个层/块的数学原理的四个方程进行连接。
上图中有许多内容,但跟随彩色线条和箭头可以揭示ViT架构的主要概念。
我们进一步分解每个方程如何(我们的目标是使用代码重新创建这些方程)?
在所有方程(除了方程4)中,“$\mathbf{z}$”是特定层的原始输出:
- $\mathbf{z}_{0}$ 是 "z零"(这是初始图像块嵌入层的输出)。
- $\mathbf{z}_{\ell}^{\prime}$ 是 "z特定层 prime"(或z的中间值)。
- $\mathbf{z}_{\ell}$ 是 "z特定层"。
而 $\mathbf{y}$ 是架构的整体输出。
3.2.3 公式1概述¶
$$ \begin{aligned} \mathbf{z}_{0} &=\left[\mathbf{x}_{\text {class }} ; \mathbf{x}_{p}^{1} \mathbf{E} ; \mathbf{x}_{p}^{2} \mathbf{E} ; \cdots ; \mathbf{x}_{p}^{N} \mathbf{E}\right]+\mathbf{E}_{\text {pos }}, & & \mathbf{E} \in \mathbb{R}^{\left(P^{2} \cdot C\right) \times D}, \mathbf{E}_{\text {pos }} \in \mathbb{R}^{(N+1) \times D} \end{aligned} $$
该公式处理输入图像的类别标记、分块嵌入和位置嵌入($\mathbf{E}$ 表示嵌入矩阵)。
在向量形式中,嵌入可能看起来像这样:
x_input = [class_token, image_patch_1, image_patch_2, image_patch_3...] + [class_token_position, image_patch_1_position, image_patch_2_position, image_patch_3_position...]
其中向量中的每个元素都是可学习的(它们的 requires_grad=True)。
3.2.4 公式2概述¶
$$ \begin{aligned} \mathbf{z}_{\ell}^{\prime} &=\operatorname{MSA}\left(\operatorname{LN}\left(\mathbf{z}_{\ell-1}\right)\right)+\mathbf{z}_{\ell-1}, & & \ell=1 \ldots L \end{aligned} $$
这表示对于从第1层到第$L$层(总层数)的每一层,都有一个多头注意力层(MSA)包裹着一个层归一化层(LN)。
末尾的加法相当于将输入与输出相加,形成一个跳跃/残差连接。
我们称这一层为“MSA块”。
用伪代码表示,这可能看起来像:
x_output_MSA_block = MSA_layer(LN_layer(x_input)) + x_input
注意末尾的跳跃连接(将层的输入与层的输出相加)。
3.2.5 公式3概述¶
$$ \begin{aligned} \mathbf{z}_{\ell} &=\operatorname{MLP}\left(\operatorname{LN}\left(\mathbf{z}_{\ell}^{\prime}\right)\right)+\mathbf{z}_{\ell}^{\prime}, & & \ell=1 \ldots L \\ \end{aligned} $$
这表示对于从第1层到第$L$层(总层数),每一层都有一个多层感知机(MLP)层包裹着一个层归一化(LN)层。
末尾的加法表示存在一个跳跃/残差连接。
我们称这一层为“MLP块”。
在伪代码中,这可能看起来像:
x_output_MLP_block = MLP_layer(LN_layer(x_output_MSA_block)) + x_output_MSA_block
注意末尾的跳跃连接(将层的输入与层的输出相加)。
3.2.6 公式4概述¶
$$ \begin{aligned} \mathbf{y} &=\operatorname{LN}\left(\mathbf{z}_{L}^{0}\right) & & \end{aligned} $$
这表示对于最后一层 $L$,输出 $y$ 是 $z$ 的第0个索引标记经过 LayerNorm 层(LN)处理后的结果。
或者在我们的例子中,x_output_MLP_block 的第0个索引:
y = Linear_layer(LN_layer(x_output_MLP_block[0]))
当然,上述内容有一些简化,但我们会在编写每个部分的 PyTorch 代码时处理这些细节。
注意: 上述部分涵盖了大量信息。但请记住,如果有不理解的地方,你总是可以进一步研究。例如,可以通过提问“什么是残差连接?”来深入了解。
3.2.7 探索表1¶
我们将关注的ViT架构的最后一部分(目前)是表1。
| 模型 | 层数 | 隐藏层大小 $D$ | MLP大小 | 头数 | 参数数量 |
|---|---|---|---|---|---|
| ViT-Base | 12 | 768 | 3072 | 12 | $86M$ |
| ViT-Large | 24 | 1024 | 4096 | 16 | $307M$ |
| ViT-Huge | 32 | 1280 | 5120 | 16 | $632M$ |
此表展示了每种ViT架构的各种超参数。
你可以看到从ViT-Base到ViT-Huge,数值逐渐增加。
我们将专注于复现ViT-Base(从小规模开始,必要时再扩展),但我们将编写可以轻松扩展到更大变体的代码。
分解这些超参数:
- 层数 - 有多少个Transformer编码器块?(每个块包含一个MSA块和一个MLP块)
- 隐藏层大小 $D$ - 这是整个架构中的嵌入维度,这将是我们图像在被分块和嵌入时的向量大小。通常,嵌入维度越大,可以捕获的信息越多,结果越好。然而,更大的嵌入维度会增加计算成本。
- MLP大小 - MLP层中的隐藏单元数量是多少?
- 头数 - 多头注意力层中有多少个头?
- 参数数量 - 模型的总参数数量是多少?通常,更多的参数会带来更好的性能,但会增加计算成本。你会注意到,即使是ViT-Base,其参数数量也远超我们之前使用的任何模型。
我们将使用这些值作为我们ViT架构的超参数设置。
3.3 我复现论文的工作流程¶
当我开始着手复现一篇论文时,我会按照以下步骤进行:
- 从头到尾阅读整篇论文一次(以了解主要概念)。
- 回顾每个部分,看看它们是如何相互关联的,并开始思考如何将它们转化为代码(就像上面那样)。
- 重复步骤2,直到我有了一个相当好的大纲。
- 使用 mathpix.com(一个非常方便的工具)将论文的任何部分转换为markdown/LaTeX,以便放入笔记本中。
- 复现尽可能简单的模型版本。
- 如果遇到困难,查找其他示例。

使用 mathpix.com 将 ViT 论文中的四个方程转换为可编辑的 LaTeX/markdown。
我们已经完成了上述的前几个步骤(如果你还没有阅读完整篇论文,我鼓励你去尝试一下),但我们接下来将重点关注步骤5:复现尽可能简单的模型版本。
这就是我们为什么从 ViT-Base 开始的原因。
复现尽可能小的架构版本,让它运行起来,然后如果我们愿意,可以再进行扩展。
注意: 如果你以前从未阅读过研究论文,上述许多步骤可能会让人感到畏惧。但别担心,像任何事情一样,你阅读和复现论文的技能会随着练习而提高。别忘了,一篇研究论文通常是许多人几个月工作的成果压缩在几页纸上。所以尝试自己复现它绝非易事。
4. 方程1:将数据分割成块并创建类别、位置和块嵌入¶
我记得我的一位机器学习工程师朋友曾经说过:“一切都与嵌入有关。”
也就是说,如果你能以一种好的、可学习的方式(如嵌入是可学习的表示)来表示你的数据,那么一个学习算法很可能会在这些数据上表现良好。
话虽如此,让我们开始为ViT架构创建类别、位置和块嵌入。
我们将从块嵌入开始。
这意味着我们将把输入图像转换成一系列的块,然后嵌入这些块。
回想一下,嵌入是某种形式的可学习表示,通常是一个向量。
“可学习”这个词很重要,因为这意味着输入图像的数值表示(模型所看到的)可以随着时间的推移而改进。
我们将从ViT论文第3.1节的引言段落开始(加粗部分为我所强调):
标准的Transformer接收一个1D序列的标记嵌入作为输入。为了处理2D图像,我们将图像$\mathbf{x} \in \mathbb{R}^{H \times W \times C}$重塑为一个扁平化的2D块序列$\mathbf{x}_{p} \in \mathbb{R}^{N \times\left(P^{2} \cdot C\right)}$,其中$(H, W)$是原始图像的分辨率,$C$是通道数,$(P, P)$是每个图像块的分辨率,$N=H W / P^{2}$是生成的块数,这也作为Transformer的有效输入序列长度。Transformer在其所有层中使用恒定的潜在向量大小$D$,因此我们扁平化这些块并通过一个可训练的线性投影映射到$D$维(方程1)。我们将这个投影的输出称为块嵌入。
并且考虑到我们处理的图像形状,让我们记住ViT论文表3中的一行:
训练分辨率为224。
让我们分解上面的文本。
- $D$ 是块嵌入的大小,不同大小的ViT模型对应的$D$值可以在表1中找到。
- 图像最初是2D的,大小为${H \times W \times C}$。
- $(H, W)$ 是原始图像的分辨率(高度,宽度)。
- $C$ 是通道数。
- 图像被转换为一系列扁平化的2D块,大小为${N \times\left(P^{2} \cdot C\right)}$。
- $(P, P)$ 是每个图像块的分辨率(块大小)。
- $N=H W / P^{2}$ 是生成的块数,这也作为Transformer的输入序列长度。
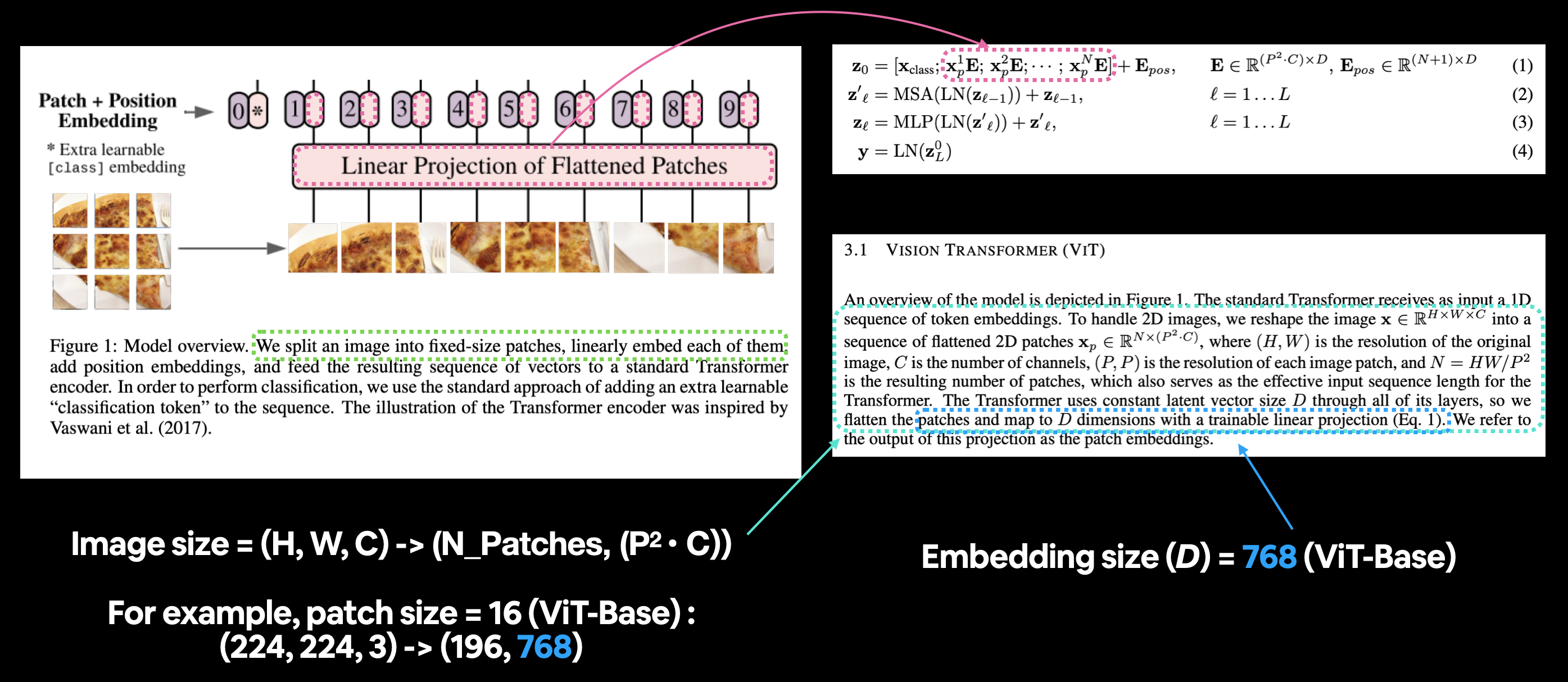
将图1中ViT架构的块和位置嵌入部分映射到方程1。第3.1节的引言段落描述了块嵌入层的不同输入和输出形状。
4.1 手动计算补丁嵌入的输入和输出形状¶
让我们从手动计算这些输入和输出形状值开始吧。
为此,我们创建一些变量来模拟上述各个术语(如 $H$、$W$ 等)。
我们将使用 16 的补丁大小($P$),因为这是 ViT-Base 表现最好的版本所使用的(更多信息请参见 ViT 论文中表 5 的“ViT-B/16”列)。
# Create example values
height = 224 # H ("The training resolution is 224.")
width = 224 # W
color_channels = 3 # C
patch_size = 16 # P
# Calculate N (number of patches)
number_of_patches = int((height * width) / patch_size**2)
print(f"Number of patches (N) with image height (H={height}), width (W={width}) and patch size (P={patch_size}): {number_of_patches}")
Number of patches (N) with image height (H=224), width (W=224) and patch size (P=16): 196
我们已经得到了补丁的数量,那么我们是否也可以创建输出图像的大小呢?
更好的是,让我们复制补丁嵌入层的输入和输出形状。
回顾一下:
- 输入: 图像最初是二维的,大小为 ${H \times W \times C}$。
- 输出: 图像被转换为一系列展平的二维补丁,大小为 ${N \times\left(P^{2} \cdot C\right)}$。
# Input shape (this is the size of a single image)
embedding_layer_input_shape = (height, width, color_channels)
# Output shape
embedding_layer_output_shape = (number_of_patches, patch_size**2 * color_channels)
print(f"Input shape (single 2D image): {embedding_layer_input_shape}")
print(f"Output shape (single 2D image flattened into patches): {embedding_layer_output_shape}")
Input shape (single 2D image): (224, 224, 3) Output shape (single 2D image flattened into patches): (196, 768)
输入和输出形状已获取!
4.2 将单张图像转换为图像块¶
现在我们知道了图像块嵌入层的理想输入和输出形状,接下来让我们着手实现它。
我们的做法是将整体架构分解为更小的部分,重点关注各个层的输入和输出。
那么,我们如何创建图像块嵌入层呢?
我们很快就会讲到这一点,首先,让我们可视化,可视化,再可视化!看看将图像转换为图像块是什么样子的。
让我们从单张图像开始。
# View single image
plt.imshow(image.permute(1, 2, 0)) # adjust for matplotlib
plt.title(class_names[label])
plt.axis(False);
我们希望将这张图像转换成与ViT论文中图1所示的内联图像块。
不如我们先从可视化最上面一行的图像块像素开始?
我们可以通过索引不同的图像维度来实现这一点。
# Change image shape to be compatible with matplotlib (color_channels, height, width) -> (height, width, color_channels)
image_permuted = image.permute(1, 2, 0)
# Index to plot the top row of patched pixels
patch_size = 16
plt.figure(figsize=(patch_size, patch_size))
plt.imshow(image_permuted[:patch_size, :, :]);
现在我们已经有了顶行,接下来将其转换为小块。
我们可以通过迭代顶行中将会有的小块数量来实现这一点。
# Setup hyperparameters and make sure img_size and patch_size are compatible
img_size = 224
patch_size = 16
num_patches = img_size/patch_size
assert img_size % patch_size == 0, "Image size must be divisible by patch size"
print(f"Number of patches per row: {num_patches}\nPatch size: {patch_size} pixels x {patch_size} pixels")
# Create a series of subplots
fig, axs = plt.subplots(nrows=1,
ncols=img_size // patch_size, # one column for each patch
figsize=(num_patches, num_patches),
sharex=True,
sharey=True)
# Iterate through number of patches in the top row
for i, patch in enumerate(range(0, img_size, patch_size)):
axs[i].imshow(image_permuted[:patch_size, patch:patch+patch_size, :]); # keep height index constant, alter the width index
axs[i].set_xlabel(i+1) # set the label
axs[i].set_xticks([])
axs[i].set_yticks([])
Number of patches per row: 14.0 Patch size: 16 pixels x 16 pixels
这些补丁看起来很不错!
我们何不将整个图像都这样做呢?
这次我们将遍历高度和宽度的索引,并将每个补丁绘制在自己的子图中。
# Setup hyperparameters and make sure img_size and patch_size are compatible
img_size = 224
patch_size = 16
num_patches = img_size/patch_size
assert img_size % patch_size == 0, "Image size must be divisible by patch size"
print(f"Number of patches per row: {num_patches}\
\nNumber of patches per column: {num_patches}\
\nTotal patches: {num_patches*num_patches}\
\nPatch size: {patch_size} pixels x {patch_size} pixels")
# Create a series of subplots
fig, axs = plt.subplots(nrows=img_size // patch_size, # need int not float
ncols=img_size // patch_size,
figsize=(num_patches, num_patches),
sharex=True,
sharey=True)
# Loop through height and width of image
for i, patch_height in enumerate(range(0, img_size, patch_size)): # iterate through height
for j, patch_width in enumerate(range(0, img_size, patch_size)): # iterate through width
# Plot the permuted image patch (image_permuted -> (Height, Width, Color Channels))
axs[i, j].imshow(image_permuted[patch_height:patch_height+patch_size, # iterate through height
patch_width:patch_width+patch_size, # iterate through width
:]) # get all color channels
# Set up label information, remove the ticks for clarity and set labels to outside
axs[i, j].set_ylabel(i+1,
rotation="horizontal",
horizontalalignment="right",
verticalalignment="center")
axs[i, j].set_xlabel(j+1)
axs[i, j].set_xticks([])
axs[i, j].set_yticks([])
axs[i, j].label_outer()
# Set a super title
fig.suptitle(f"{class_names[label]} -> Patchified", fontsize=16)
plt.show()
Number of patches per row: 14.0 Number of patches per column: 14.0 Total patches: 196.0 Patch size: 16 pixels x 16 pixels
图像被分块了!
哇,看起来很酷。
现在我们如何将每个分块转换为嵌入并将其转换为序列呢?
提示:我们可以使用PyTorch层。你能猜到是哪些吗?
4.3 使用 torch.nn.Conv2d() 创建图像块¶
我们已经了解了图像在转换为图像块时的样子,现在让我们开始使用 PyTorch 来复现这些图像块嵌入层。
为了可视化单张图像,我们编写了代码来遍历单张图像的不同高度和宽度维度,并绘制单个图像块。
这个操作与我们之前在 03. PyTorch 计算机视觉章节 7.1:逐步解析 nn.Conv2d() 中看到的卷积操作非常相似。
事实上,ViT 论文的作者在第 3.1 节中提到,可以使用卷积神经网络(CNN)来实现图像块嵌入:
混合架构。 作为原始图像块的替代方案,输入序列可以由 CNN 的特征图(LeCun 等人,1989)形成。在这种混合模型中,图像块嵌入投影 $\mathbf{E}$(公式 1)应用于从 CNN 特征图 中提取的图像块。作为一种特殊情况,图像块可以具有空间大小 $1 \times 1$,这意味着 输入序列是通过简单地展平特征图的空间维度并投影到 Transformer 维度 获得的。如上所述,添加分类输入嵌入和位置嵌入。
他们提到的“特征图”是由卷积层在给定图像上生成的权重/激活。

通过将 torch.nn.Conv2d() 层的 kernel_size 和 stride 参数设置为 patch_size,我们可以有效地获得一个将图像分割成图像块并创建每个图像块的可学习嵌入(在 ViT 论文中称为“线性投影”)的层。
还记得我们理想的图像块嵌入层的输入和输出形状吗?
- 输入: 图像开始时是 2D 的,大小为 ${H \times W \times C}$。
- 输出: 图像被转换为展平的 2D 图像块的 1D 序列,大小为 ${N \times\left(P^{2} \cdot C\right)}$。
或者对于大小为 224 和图像块大小为 16 的图像:
- 输入(2D 图像): (224, 224, 3) -> (高度, 宽度, 颜色通道)
- 输出(展平的 2D 图像块): (196, 768) -> (图像块数量, 嵌入维度)
我们可以使用以下方法来复现这些操作:
torch.nn.Conv2d()将图像转换为 CNN 特征图的图像块。torch.nn.Flatten()展平特征图的空间维度。
让我们从 torch.nn.Conv2d() 层开始。
我们可以通过将 kernel_size 和 stride 设置为 patch_size 来复现图像块的创建。
这意味着每个卷积核的大小为 (patch_size x patch_size),或者如果 patch_size=16,则为 (16 x 16)(相当于一个完整的图像块)。
卷积核的每一步或 stride 将是 patch_size 像素长,即 16 像素长(相当于移动到下一个图像块)。
我们将设置 in_channels=3 表示图像的颜色通道数量,并设置 out_channels=768,这与 ViT-Base 的表 1 中的 $D$ 值相同(这是嵌入维度,每个图像将被嵌入到一个大小为 768 的可学习向量中)。
from torch import nn
# Set the patch size
patch_size=16
# Create the Conv2d layer with hyperparameters from the ViT paper
conv2d = nn.Conv2d(in_channels=3, # number of color channels
out_channels=768, # from Table 1: Hidden size D, this is the embedding size
kernel_size=patch_size, # could also use (patch_size, patch_size)
stride=patch_size,
padding=0)
现在我们有了一个卷积层,让我们看看当我们将单张图像通过它时会发生什么。
# View single image
plt.imshow(image.permute(1, 2, 0)) # adjust for matplotlib
plt.title(class_names[label])
plt.axis(False);
# Pass the image through the convolutional layer
image_out_of_conv = conv2d(image.unsqueeze(0)) # add a single batch dimension (height, width, color_channels) -> (batch, height, width, color_channels)
print(image_out_of_conv.shape)
torch.Size([1, 768, 14, 14])
将我们的图像通过卷积层处理后,它会变成一系列的 768 个(这是嵌入大小或 $D$)特征/激活图。
因此,其输出形状可以表示为:
torch.Size([1, 768, 14, 14]) -> [批次大小, 嵌入维度, 特征图高度, 特征图宽度]
让我们可视化五个随机的特征图,看看它们是什么样子的。
# Plot random 5 convolutional feature maps
import random
random_indexes = random.sample(range(0, 758), k=5) # pick 5 numbers between 0 and the embedding size
print(f"Showing random convolutional feature maps from indexes: {random_indexes}")
# Create plot
fig, axs = plt.subplots(nrows=1, ncols=5, figsize=(12, 12))
# Plot random image feature maps
for i, idx in enumerate(random_indexes):
image_conv_feature_map = image_out_of_conv[:, idx, :, :] # index on the output tensor of the convolutional layer
axs[i].imshow(image_conv_feature_map.squeeze().detach().numpy())
axs[i].set(xticklabels=[], yticklabels=[], xticks=[], yticks=[]);
Showing random convolutional feature maps from indexes: [571, 727, 734, 380, 90]
请注意,这些特征图在一定程度上都反映了原始图像,通过多观察几个,你可以开始看到不同的主要轮廓和一些主要特征。
需要注意的是,随着神经网络的学习,这些特征可能会发生变化。
正因如此,这些特征图可以被视为我们图像的一个可学习的嵌入。
让我们以数值形式查看其中一个。
# Get a single feature map in tensor form
single_feature_map = image_out_of_conv[:, 0, :, :]
single_feature_map, single_feature_map.requires_grad
(tensor([[[ 0.4732, 0.3567, 0.3377, 0.3736, 0.3208, 0.3913, 0.3464,
0.3702, 0.2541, 0.3594, 0.1984, 0.3982, 0.3741, 0.1251],
[ 0.4178, 0.4771, 0.3374, 0.3353, 0.3159, 0.4008, 0.3448,
0.3345, 0.5850, 0.4115, 0.2969, 0.2751, 0.6150, 0.4188],
[ 0.3209, 0.3776, 0.4970, 0.4272, 0.3301, 0.4787, 0.2754,
0.3726, 0.3298, 0.4631, 0.3087, 0.4915, 0.4129, 0.4592],
[ 0.4540, 0.4930, 0.5570, 0.2660, 0.2150, 0.2044, 0.2766,
0.2076, 0.3278, 0.3727, 0.2637, 0.2493, 0.2782, 0.3664],
[ 0.4920, 0.5671, 0.3298, 0.2992, 0.1437, 0.1701, 0.1554,
0.1375, 0.1377, 0.3141, 0.2694, 0.2771, 0.2412, 0.3700],
[ 0.5783, 0.5790, 0.4229, 0.5032, 0.1216, 0.1000, 0.0356,
0.1258, -0.0023, 0.1640, 0.2809, 0.2418, 0.2606, 0.3787],
[ 0.5334, 0.5645, 0.4781, 0.3307, 0.2391, 0.0461, 0.0095,
0.0542, 0.1012, 0.1331, 0.2446, 0.2526, 0.3323, 0.4120],
[ 0.5724, 0.2840, 0.5188, 0.3934, 0.1328, 0.0776, 0.0235,
0.1366, 0.3149, 0.2200, 0.2793, 0.2351, 0.4722, 0.4785],
[ 0.4009, 0.4570, 0.4972, 0.5785, 0.2261, 0.1447, -0.0028,
0.2772, 0.2697, 0.4008, 0.3606, 0.3372, 0.4535, 0.4492],
[ 0.5678, 0.5870, 0.5824, 0.3438, 0.5113, 0.0757, 0.1772,
0.3677, 0.3572, 0.3742, 0.3820, 0.4868, 0.3781, 0.4694],
[ 0.5845, 0.5877, 0.5826, 0.3212, 0.5276, 0.4840, 0.4825,
0.5523, 0.5308, 0.5085, 0.5606, 0.5720, 0.4928, 0.5581],
[ 0.5853, 0.5849, 0.5793, 0.3410, 0.4428, 0.4044, 0.3275,
0.4958, 0.4366, 0.5750, 0.5494, 0.5868, 0.5557, 0.5069],
[ 0.5880, 0.5888, 0.5796, 0.3377, 0.2635, 0.2347, 0.3145,
0.3486, 0.5158, 0.5722, 0.5347, 0.5753, 0.5816, 0.4378],
[ 0.5692, 0.5843, 0.5721, 0.5081, 0.2694, 0.2032, 0.1589,
0.3464, 0.5349, 0.5768, 0.5739, 0.5764, 0.5394, 0.4482]]],
grad_fn=<SliceBackward0>),
True)
single_feature_map 的 grad_fn 输出以及 requires_grad=True 属性意味着 PyTorch 正在跟踪此特征图的梯度,并且在训练过程中将通过梯度下降对其进行更新。
4.4 使用 torch.nn.Flatten() 展平 patch embedding¶
我们已经将图像转换为 patch embedding,但它们仍然是二维格式。
如何将它们转换为 ViT 模型中 patch embedding 层的期望输出形状呢?
- 期望输出(展平的二维 patch 的一维序列): (196, 768) -> (patch 数量,嵌入维度) -> ${N \times\left(P^{2} \cdot C\right)}$
让我们检查当前的形状。
# Current tensor shape
print(f"Current tensor shape: {image_out_of_conv.shape} -> [batch, embedding_dim, feature_map_height, feature_map_width]")
Current tensor shape: torch.Size([1, 768, 14, 14]) -> [batch, embedding_dim, feature_map_height, feature_map_width]
好的,我们已经得到了 768 部分($(P^{2} \cdot C)$),但我们还需要补丁的数量($N$)。
回顾 ViT 论文的第 3.1 节,它提到(加粗部分为我所加):
作为一种特殊情况,补丁可以具有 $1 \times 1$ 的空间大小,这意味着输入序列是通过简单地展平特征图的空间维度并投影到 Transformer 维度来获得的。
展平特征图的空间维度,对吧?
在 PyTorch 中,我们有什么层可以用来展平呢?
但我们不想展平整个张量,我们只想展平“特征图的空间维度”。
在我们的例子中,这指的是 image_out_of_conv 的 feature_map_height 和 feature_map_width 维度。
那么,我们可以创建一个 torch.nn.Flatten() 层,只展平这些维度,我们可以使用 start_dim 和 end_dim 参数来设置这一点吗?
# Create flatten layer
flatten = nn.Flatten(start_dim=2, # flatten feature_map_height (dimension 2)
end_dim=3) # flatten feature_map_width (dimension 3)
太棒了!现在让我们把它们整合起来!
我们将:
- 取一张图像。
- 通过卷积层(
conv2d)将图像转换为二维特征图(patch embeddings)。 - 将二维特征图展平成一个序列。
# 1. View single image
plt.imshow(image.permute(1, 2, 0)) # adjust for matplotlib
plt.title(class_names[label])
plt.axis(False);
print(f"Original image shape: {image.shape}")
# 2. Turn image into feature maps
image_out_of_conv = conv2d(image.unsqueeze(0)) # add batch dimension to avoid shape errors
print(f"Image feature map shape: {image_out_of_conv.shape}")
# 3. Flatten the feature maps
image_out_of_conv_flattened = flatten(image_out_of_conv)
print(f"Flattened image feature map shape: {image_out_of_conv_flattened.shape}")
Original image shape: torch.Size([3, 224, 224]) Image feature map shape: torch.Size([1, 768, 14, 14]) Flattened image feature map shape: torch.Size([1, 768, 196])
哇哦!看起来我们的 image_out_of_conv_flattened 形状非常接近我们期望的输出形状:
- 期望的输出(展平的2D块): (196, 768) -> ${N \times\left(P^{2} \cdot C\right)}$
- 当前形状: (1, 768, 196)
唯一的区别是当前形状包含一个批次大小,并且维度顺序与期望的输出不同。
我们该如何解决这个问题呢?
嗯,我们可以重新排列维度,对吧?
我们可以使用 torch.Tensor.permute() 来实现这一点,就像我们在使用 matplotlib 绘制图像张量时重新排列维度一样。
让我们试试看。
# Get flattened image patch embeddings in right shape
image_out_of_conv_flattened_reshaped = image_out_of_conv_flattened.permute(0, 2, 1) # [batch_size, P^2•C, N] -> [batch_size, N, P^2•C]
print(f"Patch embedding sequence shape: {image_out_of_conv_flattened_reshaped.shape} -> [batch_size, num_patches, embedding_size]")
Patch embedding sequence shape: torch.Size([1, 196, 768]) -> [batch_size, num_patches, embedding_size]
太棒了!
我们已经使用几个 PyTorch 层成功匹配了 ViT 架构中 patch embedding 层的期望输入和输出形状。
接下来,我们是否可以可视化其中一个展平的特征图呢?
# Get a single flattened feature map
single_flattened_feature_map = image_out_of_conv_flattened_reshaped[:, :, 0] # index: (batch_size, number_of_patches, embedding_dimension)
# Plot the flattened feature map visually
plt.figure(figsize=(22, 22))
plt.imshow(single_flattened_feature_map.detach().numpy())
plt.title(f"Flattened feature map shape: {single_flattened_feature_map.shape}")
plt.axis(False);
嗯,从视觉上看,这个展平的特征图似乎并不起眼,但这并不是我们关注的重点。这将是补丁嵌入层的输出,同时也是ViT架构其余部分的输入。
注意: 原始的Transformer架构 是为处理文本而设计的。而Vision Transformer架构(ViT)的目标是利用原始的Transformer来处理图像。这就是为什么ViT架构的输入需要以这种方式进行处理。我们实际上是在将一个2D图像格式化,使其呈现为1D的文本序列。
我们来看看这个展平的特征图在张量形式下是什么样的吧?
# See the flattened feature map as a tensor
single_flattened_feature_map, single_flattened_feature_map.requires_grad, single_flattened_feature_map.shape
(tensor([[ 0.4732, 0.3567, 0.3377, 0.3736, 0.3208, 0.3913, 0.3464, 0.3702,
0.2541, 0.3594, 0.1984, 0.3982, 0.3741, 0.1251, 0.4178, 0.4771,
0.3374, 0.3353, 0.3159, 0.4008, 0.3448, 0.3345, 0.5850, 0.4115,
0.2969, 0.2751, 0.6150, 0.4188, 0.3209, 0.3776, 0.4970, 0.4272,
0.3301, 0.4787, 0.2754, 0.3726, 0.3298, 0.4631, 0.3087, 0.4915,
0.4129, 0.4592, 0.4540, 0.4930, 0.5570, 0.2660, 0.2150, 0.2044,
0.2766, 0.2076, 0.3278, 0.3727, 0.2637, 0.2493, 0.2782, 0.3664,
0.4920, 0.5671, 0.3298, 0.2992, 0.1437, 0.1701, 0.1554, 0.1375,
0.1377, 0.3141, 0.2694, 0.2771, 0.2412, 0.3700, 0.5783, 0.5790,
0.4229, 0.5032, 0.1216, 0.1000, 0.0356, 0.1258, -0.0023, 0.1640,
0.2809, 0.2418, 0.2606, 0.3787, 0.5334, 0.5645, 0.4781, 0.3307,
0.2391, 0.0461, 0.0095, 0.0542, 0.1012, 0.1331, 0.2446, 0.2526,
0.3323, 0.4120, 0.5724, 0.2840, 0.5188, 0.3934, 0.1328, 0.0776,
0.0235, 0.1366, 0.3149, 0.2200, 0.2793, 0.2351, 0.4722, 0.4785,
0.4009, 0.4570, 0.4972, 0.5785, 0.2261, 0.1447, -0.0028, 0.2772,
0.2697, 0.4008, 0.3606, 0.3372, 0.4535, 0.4492, 0.5678, 0.5870,
0.5824, 0.3438, 0.5113, 0.0757, 0.1772, 0.3677, 0.3572, 0.3742,
0.3820, 0.4868, 0.3781, 0.4694, 0.5845, 0.5877, 0.5826, 0.3212,
0.5276, 0.4840, 0.4825, 0.5523, 0.5308, 0.5085, 0.5606, 0.5720,
0.4928, 0.5581, 0.5853, 0.5849, 0.5793, 0.3410, 0.4428, 0.4044,
0.3275, 0.4958, 0.4366, 0.5750, 0.5494, 0.5868, 0.5557, 0.5069,
0.5880, 0.5888, 0.5796, 0.3377, 0.2635, 0.2347, 0.3145, 0.3486,
0.5158, 0.5722, 0.5347, 0.5753, 0.5816, 0.4378, 0.5692, 0.5843,
0.5721, 0.5081, 0.2694, 0.2032, 0.1589, 0.3464, 0.5349, 0.5768,
0.5739, 0.5764, 0.5394, 0.4482]], grad_fn=<SelectBackward0>),
True,
torch.Size([1, 196]))
太棒了!
我们已经将单一的2D图像转换成了一维的可学习嵌入向量(或者在ViT论文图1中称为“展平补丁的线性投影”)。
4.5 将ViT的patch嵌入层转化为PyTorch模块¶
现在是时候将我们为创建patch嵌入所做的所有工作整合到一个PyTorch层中了。
我们可以通过子类化nn.Module并创建一个小型的PyTorch“模型”来完成上述所有步骤。
具体来说,我们将:
- 创建一个名为
PatchEmbedding的类,该类继承自nn.Module(以便它可以作为PyTorch层使用)。 - 使用参数
in_channels=3、patch_size=16(适用于ViT-Base)和embedding_dim=768(这是表1中ViT-Base的$D$)初始化该类。 - 创建一个层,使用
nn.Conv2d()将图像转换为patches(就像在4.3中一样)。 - 创建一个层,将patch特征图展平为一维(就像在4.4中一样)。
- 定义一个
forward()方法,接收输入并将其通过第3和第4步创建的层。 - 确保输出形状符合ViT架构所需的输出形状(${N \times\left(P^{2} \cdot C\right)}$)。
让我们开始吧!
# 1. Create a class which subclasses nn.Module
class PatchEmbedding(nn.Module):
"""Turns a 2D input image into a 1D sequence learnable embedding vector.
Args:
in_channels (int): Number of color channels for the input images. Defaults to 3.
patch_size (int): Size of patches to convert input image into. Defaults to 16.
embedding_dim (int): Size of embedding to turn image into. Defaults to 768.
"""
# 2. Initialize the class with appropriate variables
def __init__(self,
in_channels:int=3,
patch_size:int=16,
embedding_dim:int=768):
super().__init__()
# 3. Create a layer to turn an image into patches
self.patcher = nn.Conv2d(in_channels=in_channels,
out_channels=embedding_dim,
kernel_size=patch_size,
stride=patch_size,
padding=0)
# 4. Create a layer to flatten the patch feature maps into a single dimension
self.flatten = nn.Flatten(start_dim=2, # only flatten the feature map dimensions into a single vector
end_dim=3)
# 5. Define the forward method
def forward(self, x):
# Create assertion to check that inputs are the correct shape
image_resolution = x.shape[-1]
assert image_resolution % patch_size == 0, f"Input image size must be divisble by patch size, image shape: {image_resolution}, patch size: {patch_size}"
# Perform the forward pass
x_patched = self.patcher(x)
x_flattened = self.flatten(x_patched)
# 6. Make sure the output shape has the right order
return x_flattened.permute(0, 2, 1) # adjust so the embedding is on the final dimension [batch_size, P^2•C, N] -> [batch_size, N, P^2•C]
PatchEmbedding 层已创建!
让我们在一个单一图像上尝试一下。
set_seeds()
# Create an instance of patch embedding layer
patchify = PatchEmbedding(in_channels=3,
patch_size=16,
embedding_dim=768)
# Pass a single image through
print(f"Input image shape: {image.unsqueeze(0).shape}")
patch_embedded_image = patchify(image.unsqueeze(0)) # add an extra batch dimension on the 0th index, otherwise will error
print(f"Output patch embedding shape: {patch_embedded_image.shape}")
Input image shape: torch.Size([1, 3, 224, 224]) Output patch embedding shape: torch.Size([1, 196, 768])
太棒了!
输出的形状与我们期望的补丁嵌入层的理想输入和输出形状相匹配:
- 输入: 图像最初是二维的,大小为 ${H \times W \times C}$。
- 输出: 图像被转换为一维的扁平化二维补丁序列,大小为 ${N \times \left(P^{2} \cdot C\right)}$。
其中:
- $(H, W)$ 是原始图像的分辨率。
- $C$ 是通道数。
- $(P, P)$ 是每个图像补丁的分辨率(补丁大小)。
- $N = H W / P^{2}$ 是生成的补丁数量,这也作为Transformer的有效输入序列长度。
我们现在已经复制了公式1中的补丁嵌入,但没有复制类别标记/位置嵌入。
我们稍后会处理这些。
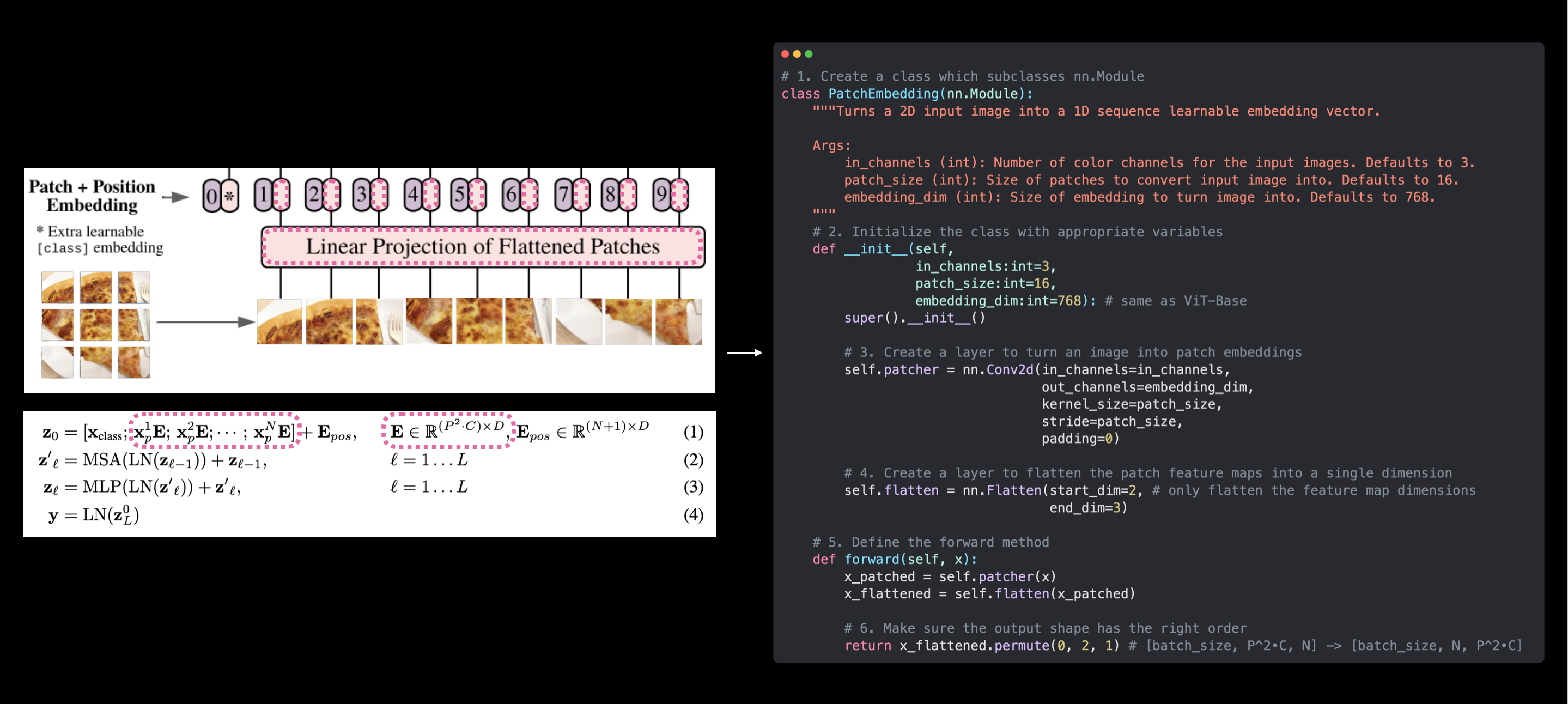
我们的 PatchEmbedding 类(右侧)复制了ViT论文中图1和公式1的ViT架构的补丁嵌入(左侧)。然而,可学习的类别嵌入和位置嵌入尚未创建。这些很快就会实现。
现在让我们来总结一下我们的 PatchEmbedding 层。
# Create random input sizes
random_input_image = (1, 3, 224, 224)
random_input_image_error = (1, 3, 250, 250) # will error because image size is incompatible with patch_size
# # Get a summary of the input and outputs of PatchEmbedding (uncomment for full output)
# summary(PatchEmbedding(),
# input_size=random_input_image, # try swapping this for "random_input_image_error"
# col_names=["input_size", "output_size", "num_params", "trainable"],
# col_width=20,
# row_settings=["var_names"])

4.6 创建类别标记嵌入¶
好的,我们已经完成了图像块嵌入,现在是时候着手处理类别标记嵌入了。
也就是方程1中的 $\mathbf{x}_\text {class }$。
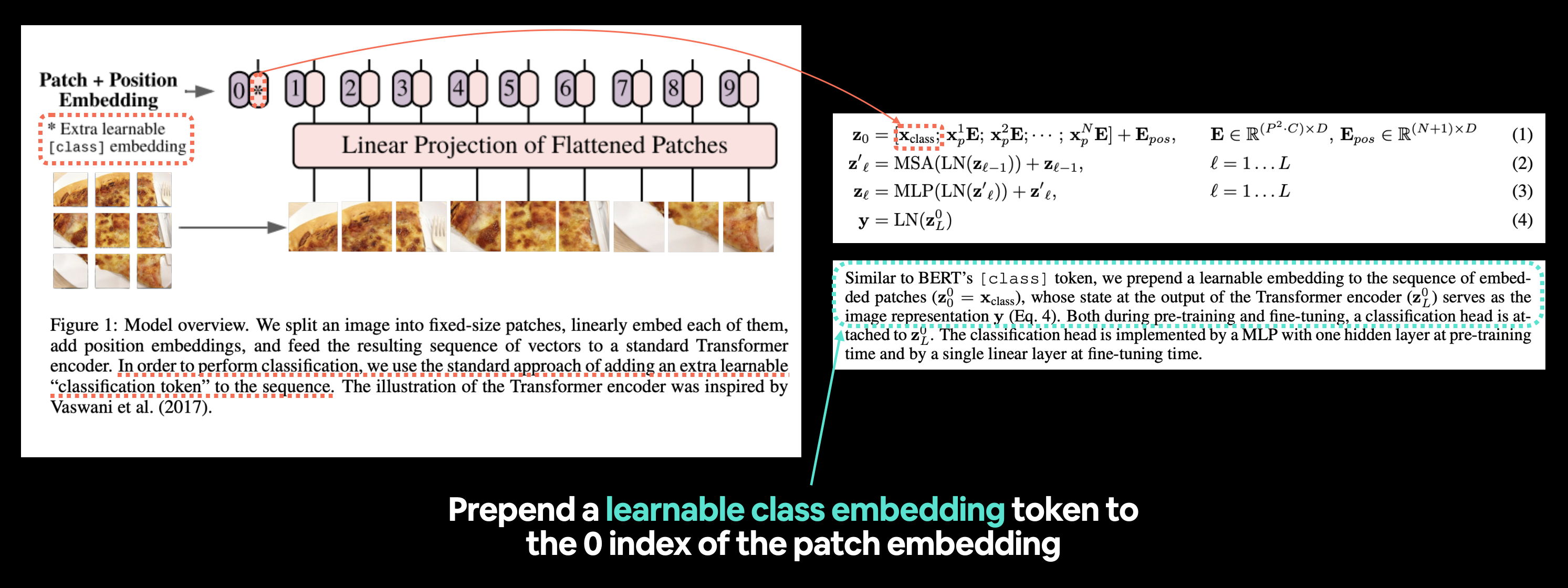
左:ViT论文中的图1,其中突出显示了我们即将重新创建的“分类标记”或[class]嵌入标记。右:ViT论文中与可学习类别嵌入标记相关的方程1和第3.1节。
阅读ViT论文第3.1节的第二段,我们看到以下描述:
类似于BERT的
[class]标记,我们在嵌入的图像块序列前添加一个可学习的嵌入 $\left(\mathbf{z}_{0}^{0}=\mathbf{x}_{\text {class }}\right)$,其在Transformer编码器输出处的状态 $\left(\mathbf{z}_{L}^{0}\right)$ 作为图像表示 $\mathbf{y}$(方程4)。
注意: BERT(来自Transformer的双向编码器表示)是最早使用Transformer架构在自然语言处理(NLP)任务中取得卓越成果的机器学习研究论文之一,也是序列开始处使用
[class]标记这一想法的起源,其中“class”是对序列所属的“分类”类别的描述。
因此,我们需要“在嵌入的图像块序列前添加一个可学习的嵌入”。
让我们先查看我们在第4.5节中创建的嵌入图像块序列张量及其形状。
# View the patch embedding and patch embedding shape
print(patch_embedded_image)
print(f"Patch embedding shape: {patch_embedded_image.shape} -> [batch_size, number_of_patches, embedding_dimension]")
tensor([[[-0.9145, 0.2454, -0.2292, ..., 0.6768, -0.4515, 0.3496],
[-0.7427, 0.1955, -0.3570, ..., 0.5823, -0.3458, 0.3261],
[-0.7589, 0.2633, -0.1695, ..., 0.5897, -0.3980, 0.0761],
...,
[-1.0072, 0.2795, -0.2804, ..., 0.7624, -0.4584, 0.3581],
[-0.9839, 0.1652, -0.1576, ..., 0.7489, -0.5478, 0.3486],
[-0.9260, 0.1383, -0.1157, ..., 0.5847, -0.4717, 0.3112]]],
grad_fn=<PermuteBackward0>)
Patch embedding shape: torch.Size([1, 196, 768]) -> [batch_size, number_of_patches, embedding_dimension]
要将"可学习的嵌入添加到嵌入的图像块序列的前面",我们需要创建一个形状为embedding_dimension($D$)的可学习嵌入,然后将其添加到number_of_patches维度上。
或者用伪代码表示:
patch_embedding = [image_patch_1, image_patch_2, image_patch_3...]
class_token = learnable_embedding
patch_embedding_with_class_token = torch.cat((class_token, patch_embedding), dim=1)
注意这里的拼接(torch.cat())发生在dim=1(即number_of_patches维度)。
接下来,我们创建一个用于类别标记的可学习嵌入。
为此,我们将获取批次大小和嵌入维度的形状,然后创建一个形状为[batch_size, 1, embedding_dimension]的torch.ones()张量。
我们将通过将该张量传递给nn.Parameter()并设置requires_grad=True,使其成为可学习的参数。
# Get the batch size and embedding dimension
batch_size = patch_embedded_image.shape[0]
embedding_dimension = patch_embedded_image.shape[-1]
# Create the class token embedding as a learnable parameter that shares the same size as the embedding dimension (D)
class_token = nn.Parameter(torch.ones(batch_size, 1, embedding_dimension), # [batch_size, number_of_tokens, embedding_dimension]
requires_grad=True) # make sure the embedding is learnable
# Show the first 10 examples of the class_token
print(class_token[:, :, :10])
# Print the class_token shape
print(f"Class token shape: {class_token.shape} -> [batch_size, number_of_tokens, embedding_dimension]")
tensor([[[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]]], grad_fn=<SliceBackward0>) Class token shape: torch.Size([1, 1, 768]) -> [batch_size, number_of_tokens, embedding_dimension]
注意: 这里我们仅出于演示目的,使用
torch.ones()创建类标记嵌入。实际上,你可能会使用torch.randn()来创建类标记嵌入(因为机器学习的核心在于利用受控随机性的力量,通常从随机数开始,并随着时间改进它)。
注意 class_token 的 number_of_tokens 维度为 1,因为我们只想在补丁嵌入序列的开头添加一个类标记值。
现在我们已经有了类标记嵌入,接下来将其添加到图像补丁序列 patch_embedded_image 的开头。
我们可以使用 torch.cat() 并设置 dim=1(这样 class_token 的 number_of_tokens 维度会添加到 patch_embedded_image 的 number_of_patches 维度之前)。
# Add the class token embedding to the front of the patch embedding
patch_embedded_image_with_class_embedding = torch.cat((class_token, patch_embedded_image),
dim=1) # concat on first dimension
# Print the sequence of patch embeddings with the prepended class token embedding
print(patch_embedded_image_with_class_embedding)
print(f"Sequence of patch embeddings with class token prepended shape: {patch_embedded_image_with_class_embedding.shape} -> [batch_size, number_of_patches, embedding_dimension]")
tensor([[[ 1.0000, 1.0000, 1.0000, ..., 1.0000, 1.0000, 1.0000],
[-0.9145, 0.2454, -0.2292, ..., 0.6768, -0.4515, 0.3496],
[-0.7427, 0.1955, -0.3570, ..., 0.5823, -0.3458, 0.3261],
...,
[-1.0072, 0.2795, -0.2804, ..., 0.7624, -0.4584, 0.3581],
[-0.9839, 0.1652, -0.1576, ..., 0.7489, -0.5478, 0.3486],
[-0.9260, 0.1383, -0.1157, ..., 0.5847, -0.4717, 0.3112]]],
grad_fn=<CatBackward0>)
Sequence of patch embeddings with class token prepended shape: torch.Size([1, 197, 768]) -> [batch_size, number_of_patches, embedding_dimension]
太棒了!可学习的类标记已添加到序列前端!

回顾我们创建可学习类标记的过程:首先,我们通过 PatchEmbedding() 对单张图像生成一系列图像块嵌入;接着,我们创建了一个可学习的类标记,其维度与嵌入维度一致;然后,我们将这个类标记添加到原始图像块嵌入序列的前端。注意: 使用 torch.ones() 来创建可学习的类标记主要是为了演示目的,实际应用中,你可能会用 torch.randn() 来创建。
4.7 创建位置嵌入¶
好的,我们已经有了类别令牌嵌入和分块嵌入,现在我们该如何创建位置嵌入呢?
也就是公式1中的 $\mathbf{E}_{\text {pos }}$,其中 $E$ 代表“嵌入”。
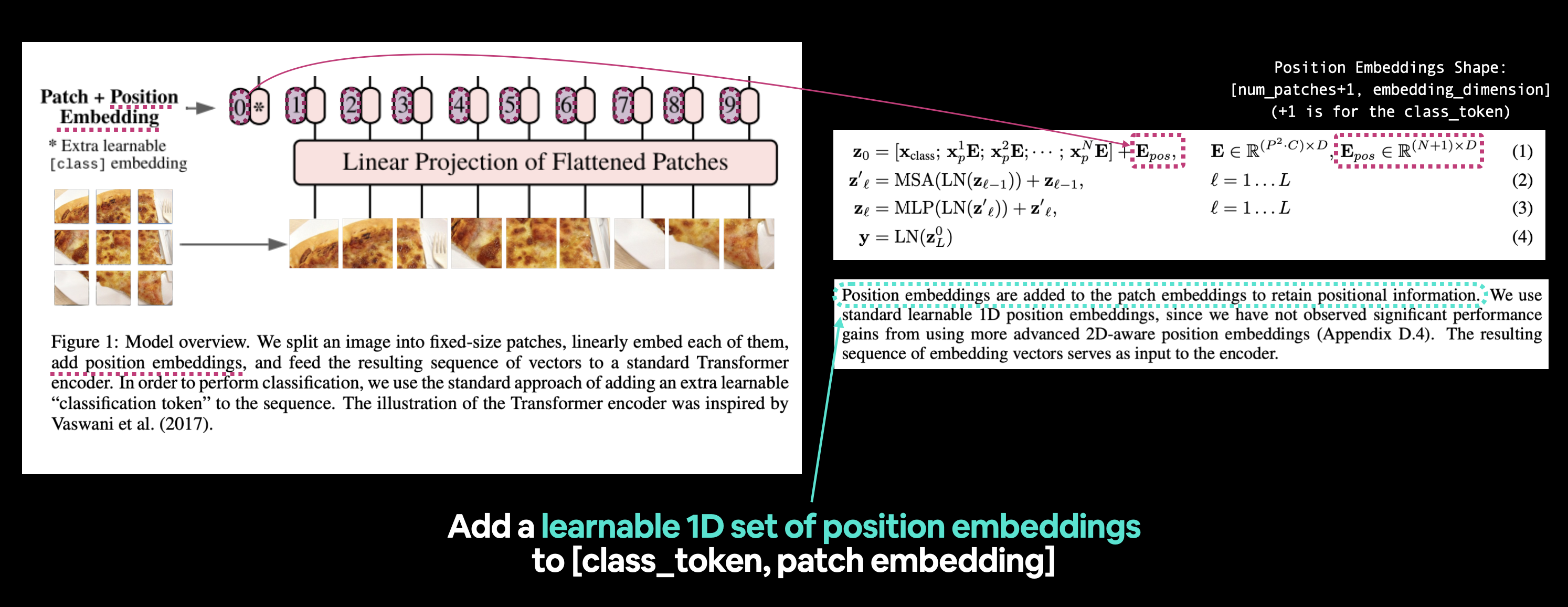
左图:来自ViT论文的图1,我们将要重现的位置嵌入部分被高亮显示。右图:公式1和ViT论文的3.1节,与位置嵌入相关。
让我们通过阅读ViT论文的3.1节来了解更多信息(加粗部分为我所加):
位置嵌入被添加到分块嵌入中以保留位置信息。我们使用标准的可学习1D位置嵌入,因为我们没有观察到使用更高级的2D感知位置嵌入会带来显著的性能提升(附录D.4)。生成的嵌入向量序列作为编码器的输入。
作者所说的“保留位置信息”意味着他们希望架构知道分块的“顺序”。也就是说,分块二紧随分块一,分块三紧随分块二,以此类推。
这种位置信息在考虑图像内容时可能很重要(没有位置信息的情况下,一个扁平化的序列可能被视为没有顺序,因此没有分块与任何其他分块相关)。
要开始创建位置嵌入,让我们先查看我们当前的嵌入。
# View the sequence of patch embeddings with the prepended class embedding
patch_embedded_image_with_class_embedding, patch_embedded_image_with_class_embedding.shape
(tensor([[[ 1.0000, 1.0000, 1.0000, ..., 1.0000, 1.0000, 1.0000],
[-0.9145, 0.2454, -0.2292, ..., 0.6768, -0.4515, 0.3496],
[-0.7427, 0.1955, -0.3570, ..., 0.5823, -0.3458, 0.3261],
...,
[-1.0072, 0.2795, -0.2804, ..., 0.7624, -0.4584, 0.3581],
[-0.9839, 0.1652, -0.1576, ..., 0.7489, -0.5478, 0.3486],
[-0.9260, 0.1383, -0.1157, ..., 0.5847, -0.4717, 0.3112]]],
grad_fn=<CatBackward0>),
torch.Size([1, 197, 768]))
公式1指出,位置嵌入($\mathbf{E}_{\text {pos }}$)的形状应为 $(N + 1) \times D$:
$$\mathbf{E}_{\text {pos }} \in \mathbb{R}^{(N+1) \times D}$$
其中:
- $N=H W / P^{2}$ 是生成的补丁数量,这也作为Transformer的有效输入序列长度(补丁数量)。
- $D$ 是补丁嵌入的大小,表1中可以找到不同的 $D$ 值(嵌入维度)。
幸运的是,这两个值我们已经有了。
因此,让我们用 torch.ones() 创建一个可学习的1D嵌入 $\mathbf{E}_{\text {pos }}$。
# Calculate N (number of patches)
number_of_patches = int((height * width) / patch_size**2)
# Get embedding dimension
embedding_dimension = patch_embedded_image_with_class_embedding.shape[2]
# Create the learnable 1D position embedding
position_embedding = nn.Parameter(torch.ones(1,
number_of_patches+1,
embedding_dimension),
requires_grad=True) # make sure it's learnable
# Show the first 10 sequences and 10 position embedding values and check the shape of the position embedding
print(position_embedding[:, :10, :10])
print(f"Position embeddding shape: {position_embedding.shape} -> [batch_size, number_of_patches, embedding_dimension]")
tensor([[[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]]], grad_fn=<SliceBackward0>)
Position embeddding shape: torch.Size([1, 197, 768]) -> [batch_size, number_of_patches, embedding_dimension]
注意: 仅出于演示目的,创建了
torch.ones()的位置嵌入,实际上,你可能会使用torch.randn()创建位置嵌入(从随机数开始并通过梯度下降进行改进)。
位置嵌入已创建!
接下来,让我们将它们添加到预先附加了类别标记的补丁嵌入序列中。
# Add the position embedding to the patch and class token embedding
patch_and_position_embedding = patch_embedded_image_with_class_embedding + position_embedding
print(patch_and_position_embedding)
print(f"Patch embeddings, class token prepended and positional embeddings added shape: {patch_and_position_embedding.shape} -> [batch_size, number_of_patches, embedding_dimension]")
tensor([[[ 2.0000, 2.0000, 2.0000, ..., 2.0000, 2.0000, 2.0000],
[ 0.0855, 1.2454, 0.7708, ..., 1.6768, 0.5485, 1.3496],
[ 0.2573, 1.1955, 0.6430, ..., 1.5823, 0.6542, 1.3261],
...,
[-0.0072, 1.2795, 0.7196, ..., 1.7624, 0.5416, 1.3581],
[ 0.0161, 1.1652, 0.8424, ..., 1.7489, 0.4522, 1.3486],
[ 0.0740, 1.1383, 0.8843, ..., 1.5847, 0.5283, 1.3112]]],
grad_fn=<AddBackward0>)
Patch embeddings, class token prepended and positional embeddings added shape: torch.Size([1, 197, 768]) -> [batch_size, number_of_patches, embedding_dimension]
注意到嵌入张量中每个元素的值都增加了1(这是因为位置嵌入是用torch.ones()创建的)。
注意: 如果我们愿意,可以将类别标记嵌入和位置嵌入分别放入它们自己的层中。但稍后我们将在第8节中看到,它们是如何被整合到ViT架构的
forward()方法中的。

我们用于将位置嵌入添加到补丁嵌入和类别标记序列中的工作流程。注意: torch.ones()仅用于创建嵌入以进行说明,实际上,您可能会使用torch.randn()来从一个随机数开始。
4.8 综合应用:从图像到嵌入¶
好了,我们已经走了很长的路,将输入图像转换为嵌入,并复现了ViT论文第3.1节中的公式1:
$$ \begin{aligned} \mathbf{z}_{0} &=\left[\mathbf{x}_{\text {class }} ; \mathbf{x}_{p}^{1} \mathbf{E} ; \mathbf{x}_{p}^{2} \mathbf{E} ; \cdots ; \mathbf{x}_{p}^{N} \mathbf{E}\right]+\mathbf{E}_{\text {pos }}, & & \mathbf{E} \in \mathbb{R}^{\left(P^{2} \cdot C\right) \times D}, \mathbf{E}_{\text {pos }} \in \mathbb{R}^{(N+1) \times D} \end{aligned} $$
现在,让我们在一个代码单元中将所有内容整合起来,从输入图像($\mathbf{x}$)到输出嵌入($\mathbf{z}_0$)。
我们可以通过以下步骤实现:
- 设置补丁大小(我们将使用
16,因为这在论文和ViT-Base模型中广泛使用)。 - 获取一张图像,打印其形状并存储其高度和宽度。
- 为单张图像添加批次维度,使其与我们的
PatchEmbedding层兼容。 - 创建一个
PatchEmbedding层(我们在第4.5节中制作的那个),设置patch_size=16和embedding_dim=768(来自ViT-Base的表1)。 - 将单张图像通过第4步中的
PatchEmbedding层,创建一系列补丁嵌入。 - 创建一个类标记嵌入,如第4.6节所示。
- 将类标记嵌入添加到第5步中创建的补丁嵌入之前。
- 创建一个位置嵌入,如第4.7节所示。
- 将位置嵌入添加到第7步中创建的类标记和补丁嵌入中。
我们还将确保使用 set_seeds() 设置随机种子,并在过程中打印不同张量的形状。
set_seeds()
# 1. Set patch size
patch_size = 16
# 2. Print shape of original image tensor and get the image dimensions
print(f"Image tensor shape: {image.shape}")
height, width = image.shape[1], image.shape[2]
# 3. Get image tensor and add batch dimension
x = image.unsqueeze(0)
print(f"Input image with batch dimension shape: {x.shape}")
# 4. Create patch embedding layer
patch_embedding_layer = PatchEmbedding(in_channels=3,
patch_size=patch_size,
embedding_dim=768)
# 5. Pass image through patch embedding layer
patch_embedding = patch_embedding_layer(x)
print(f"Patching embedding shape: {patch_embedding.shape}")
# 6. Create class token embedding
batch_size = patch_embedding.shape[0]
embedding_dimension = patch_embedding.shape[-1]
class_token = nn.Parameter(torch.ones(batch_size, 1, embedding_dimension),
requires_grad=True) # make sure it's learnable
print(f"Class token embedding shape: {class_token.shape}")
# 7. Prepend class token embedding to patch embedding
patch_embedding_class_token = torch.cat((class_token, patch_embedding), dim=1)
print(f"Patch embedding with class token shape: {patch_embedding_class_token.shape}")
# 8. Create position embedding
number_of_patches = int((height * width) / patch_size**2)
position_embedding = nn.Parameter(torch.ones(1, number_of_patches+1, embedding_dimension),
requires_grad=True) # make sure it's learnable
# 9. Add position embedding to patch embedding with class token
patch_and_position_embedding = patch_embedding_class_token + position_embedding
print(f"Patch and position embedding shape: {patch_and_position_embedding.shape}")
Image tensor shape: torch.Size([3, 224, 224]) Input image with batch dimension shape: torch.Size([1, 3, 224, 224]) Patching embedding shape: torch.Size([1, 196, 768]) Class token embedding shape: torch.Size([1, 1, 768]) Patch embedding with class token shape: torch.Size([1, 197, 768]) Patch and position embedding shape: torch.Size([1, 197, 768])
哇哦!
从单张图像到分块和位置嵌入,只需一行代码。
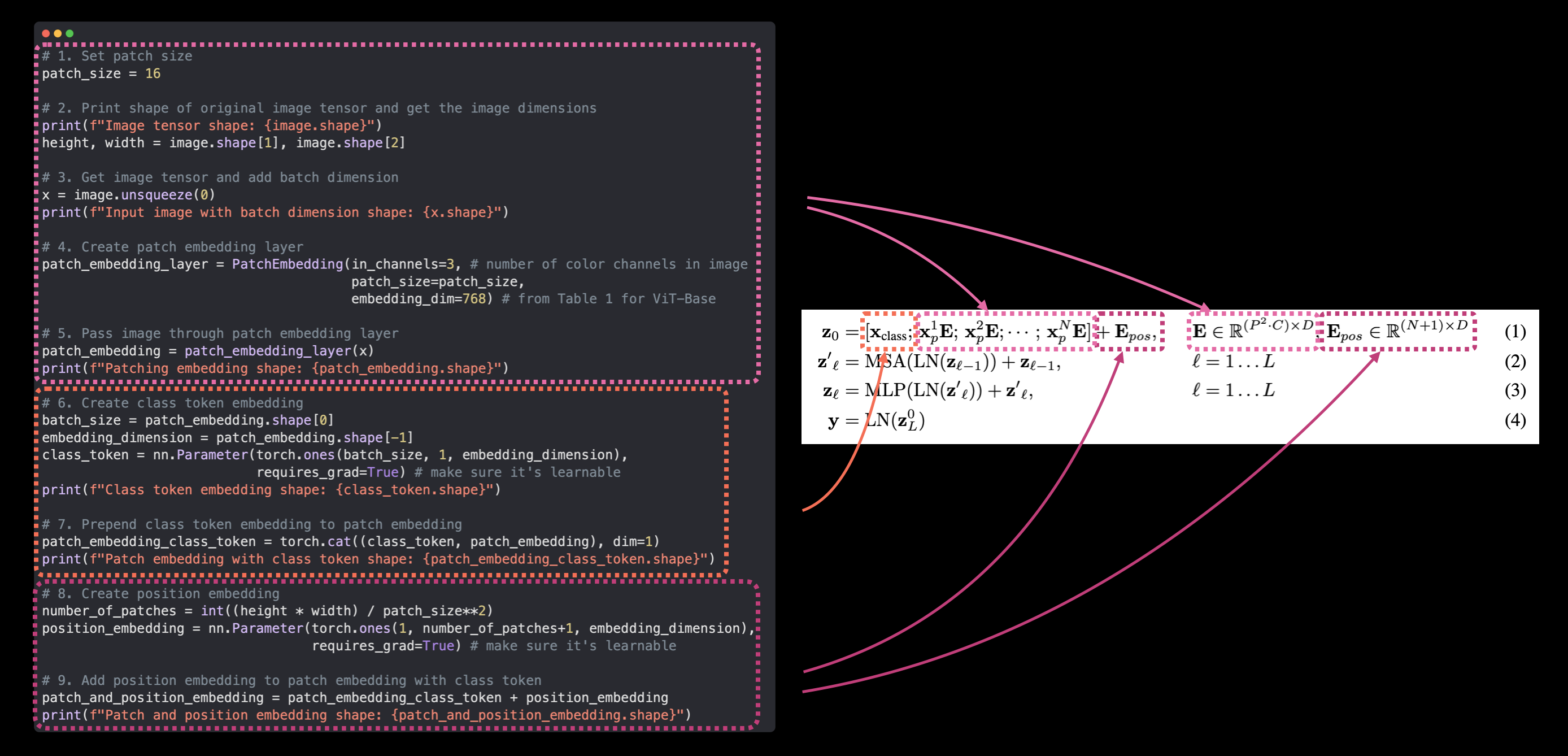
将ViT论文中的方程1映射到我们的PyTorch代码。这是复现论文的精髓,将研究论文转化为可用的代码。
现在我们已经有了一个方法来编码我们的图像,并将它们传递给ViT论文图1中的Transformer编码器。

动画展示整个ViT工作流程:从分块嵌入到Transformer编码器再到MLP头部。
从代码的角度来看,创建分块嵌入可能是复现ViT论文中最大的部分。
ViT论文中的许多其他部分,如多头注意力和归一化层,可以使用现有的PyTorch层来创建。
继续前进!
5. 方程 2:多头注意力(MSA)¶
我们已经将输入数据分块并嵌入,现在让我们继续探讨 ViT 架构的下一个部分。
首先,我们将 Transformer 编码器部分分解为两个部分(从简单开始,必要时增加复杂度)。
第一部分是方程 2,第二部分是方程 3。
回顾方程 2 的内容:
$$ \begin{aligned} \mathbf{z}_{\ell}^{\prime} &=\operatorname{MSA}\left(\operatorname{LN}\left(\mathbf{z}_{\ell-1}\right)\right)+\mathbf{z}_{\ell-1}, & & \ell=1 \ldots L \end{aligned} $$
这表示一个多头注意力(MSA)层被包裹在一个层归一化(LN)层中,并带有一个残差连接(层的输入被加到层的输出上)。
我们将方程 2 称为“MSA 块”。
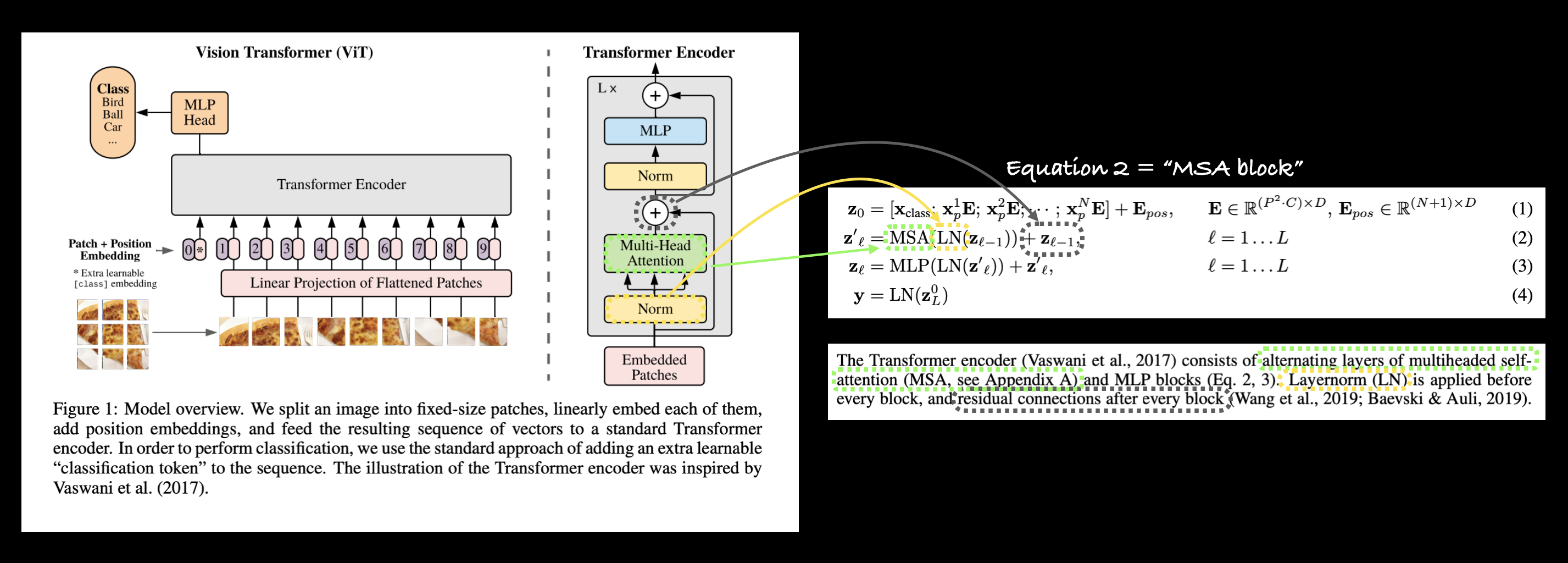
***左图:** 来自 ViT 论文的图 1,其中 Transformer 编码器块内的多头注意力和归一化层以及残差连接(+)被高亮显示。 右图: 将多头自注意力(MSA)层、归一化层和残差连接映射到 ViT 论文中方程 2 的相应部分。*
许多在研究论文中发现的层已经在现代深度学习框架中实现,例如 PyTorch。
尽管如此,为了用 PyTorch 代码复制这些层和残差连接,我们可以使用:
- 多头自注意力(MSA) -
torch.nn.MultiheadAttention()。 - 归一化(LN 或 LayerNorm) -
torch.nn.LayerNorm()。 - 残差连接 - 将输入加到输出上(我们将在第 7.1 节创建完整的 Transformer 编码器块时看到这一点)。
5.1 LayerNorm(层归一化)层¶
层归一化(torch.nn.LayerNorm() 或 Norm 或 LayerNorm 或 LN)对输入的最后一个维度进行归一化处理。
你可以在 PyTorch 文档中找到 torch.nn.LayerNorm() 的正式定义。
PyTorch 的 torch.nn.LayerNorm() 的主要参数是 normalized_shape,我们可以将其设置为我们希望归一化的维度大小(在我们的例子中,对于 ViT-Base 模型,它将是 $D$ 或 768)。
它有什么作用?
层归一化有助于改善训练时间和模型的泛化能力(适应未见数据的能力)。
我喜欢将任何类型的归一化视为“将数据转换为相似的格式”或“将数据样本转换为相似的分布”。
想象一下,试图走上(或走下)一组高度和长度各不相同的楼梯。
每一步都需要一些调整,对吧?
而且你在每一步学到的知识不一定有助于下一步,因为它们都不同,这增加了你穿越楼梯所需的时间。
归一化(包括层归一化)相当于让所有楼梯的高度和长度都相同,只不过这里的楼梯是你的数据样本。
因此,就像你走上(或走下)高度和长度相似的楼梯比那些高度和宽度不等的楼梯容易得多一样,神经网络在优化具有相似分布(相似的均值和标准差)的数据样本时,比那些分布各异的数据样本更容易。
5.2 多头自注意力(MSA)层¶
自注意力和多头注意力(多次应用自注意力)的强大能力在《注意力就是你所需要的一切》研究论文中介绍的原始Transformer架构中得到了体现。
最初设计用于文本输入,原始的自注意力机制接受一系列单词,然后计算哪个单词应该对另一个单词给予更多“关注”。
换句话说,在句子“the dog jumped over the fence”中,可能单词“dog”与“jumped”和“fence”有很强的关联。
这虽然简化了,但前提仍然适用于图像。
由于我们的输入是一系列图像块而不是单词,自注意力和随后的多头注意力将计算图像的哪个块与另一个块最相关,最终形成图像的学习表示。
但最重要的是,这一层在给定数据的情况下自行完成这一过程(我们不告诉它学习什么模式)。
如果通过MSA形成的层学习表示是好的,我们将在模型的性能中看到结果。
网上有许多资源可以了解更多关于Transformer架构和注意力机制的信息,例如Jay Alammar精彩的《Illustrated Transformer》文章和《Illustrated Attention》文章。
我们将更多地关注编写现有的PyTorch MSA实现,而不是创建我们自己的。
然而,你可以在附录A中找到ViT论文中MSA实现的正式定义:
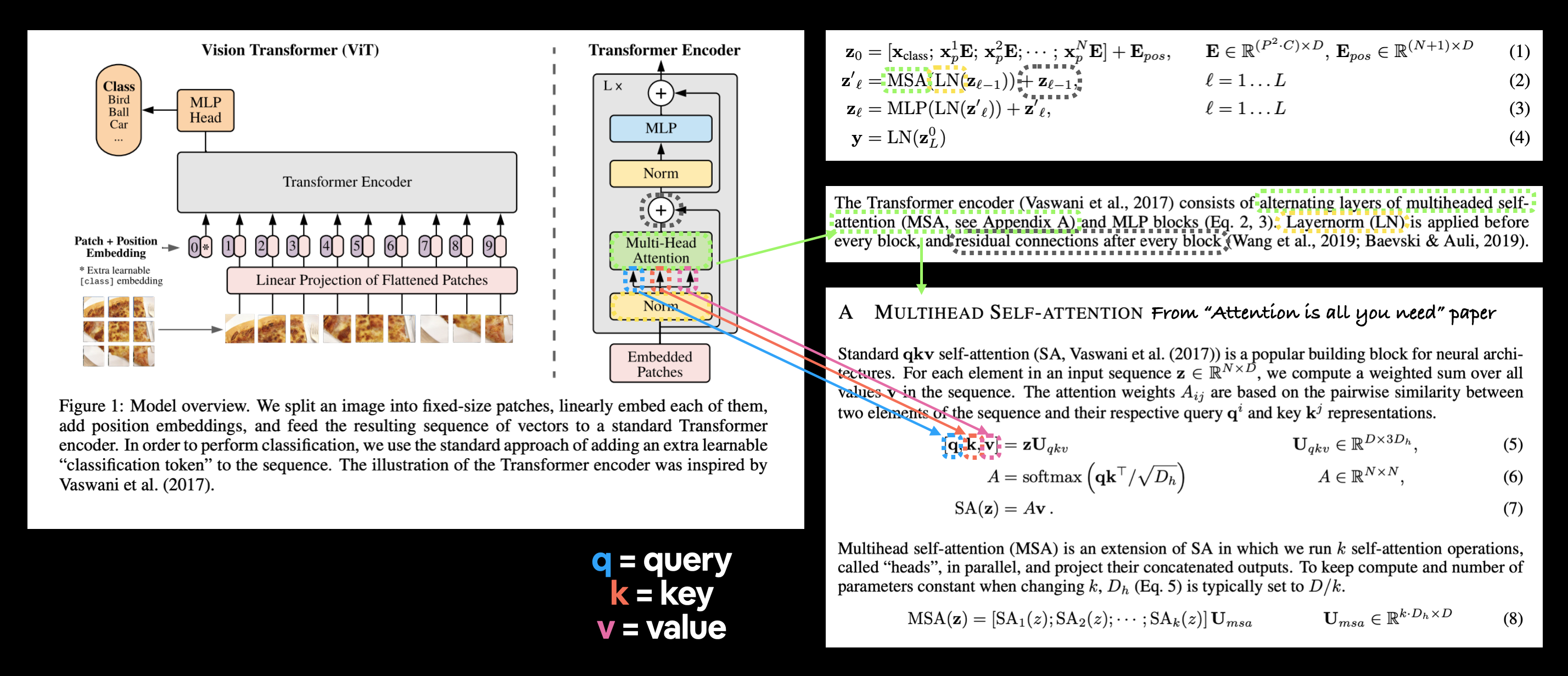
***左:** 来自ViT论文图1的Vision Transformer架构概览。 右: 突出显示了ViT论文中公式2、第3.1节和附录A的定义,以反映它们在图1中的相应部分。*
上图突出显示了输入到MSA层的三重嵌入。
这就是查询、键、值输入,简称qkv,这是自注意力机制的基础。
在我们的例子中,三重嵌入输入将是Norm层输出的三个版本,分别用于查询、键和值。
或者说是我们在第4.8节中创建的层归一化图像块和位置嵌入的三个版本。
我们可以在PyTorch中使用torch.nn.MultiheadAttention()实现MSA层,参数如下:
embed_dim- 来自表1的嵌入维度(隐藏大小$D$)。num_heads- 使用多少个注意力头(这就是“多头”这一术语的来源),这个值也在表1中(头数)。dropout- 是否对注意力层应用dropout(根据附录B.1,qkv投影后不使用dropout)。batch_first- 我们的批次维度是否在首位?(是的)
5.3 使用PyTorch层重现公式2¶
让我们将在公式2中讨论的关于层归一化(LayerNorm,LN)和多头注意力(Multi-Head Attention,MSA)层的所有内容付诸实践。
为此,我们将:
- 创建一个名为
MultiheadSelfAttentionBlock的类,该类继承自torch.nn.Module。 - 使用ViT论文中表1的ViT-Base模型的超参数初始化该类。
- 使用
torch.nn.LayerNorm()创建一个层归一化(LN)层,其normalized_shape参数与我们嵌入维度(表1中的$D$)相同。 - 使用适当的
embed_dim、num_heads、dropout和batch_first参数创建一个多头注意力(MSA)层。 - 为我们的类创建一个
forward()方法,将输入通过LN层和MSA层。
# 1. Create a class that inherits from nn.Module
class MultiheadSelfAttentionBlock(nn.Module):
"""Creates a multi-head self-attention block ("MSA block" for short).
"""
# 2. Initialize the class with hyperparameters from Table 1
def __init__(self,
embedding_dim:int=768, # Hidden size D from Table 1 for ViT-Base
num_heads:int=12, # Heads from Table 1 for ViT-Base
attn_dropout:float=0): # doesn't look like the paper uses any dropout in MSABlocks
super().__init__()
# 3. Create the Norm layer (LN)
self.layer_norm = nn.LayerNorm(normalized_shape=embedding_dim)
# 4. Create the Multi-Head Attention (MSA) layer
self.multihead_attn = nn.MultiheadAttention(embed_dim=embedding_dim,
num_heads=num_heads,
dropout=attn_dropout,
batch_first=True) # does our batch dimension come first?
# 5. Create a forward() method to pass the data throguh the layers
def forward(self, x):
x = self.layer_norm(x)
attn_output, _ = self.multihead_attn(query=x, # query embeddings
key=x, # key embeddings
value=x, # value embeddings
need_weights=False) # do we need the weights or just the layer outputs?
return attn_output
注意: 与图1不同,我们的
MultiheadSelfAttentionBlock不包含跳跃或残差连接(公式2中的“$+\mathbf{z}_{\ell-1}$”),我们将在第7.1节创建完整的Transformer编码器时添加这一部分。
MSABlock已创建!
让我们尝试创建一个 MultiheadSelfAttentionBlock 实例,并通过我们在第4.8节创建的 patch_and_position_embedding 变量传递数据。
# Create an instance of MSABlock
multihead_self_attention_block = MultiheadSelfAttentionBlock(embedding_dim=768, # from Table 1
num_heads=12) # from Table 1
# Pass patch and position image embedding through MSABlock
patched_image_through_msa_block = multihead_self_attention_block(patch_and_position_embedding)
print(f"Input shape of MSA block: {patch_and_position_embedding.shape}")
print(f"Output shape MSA block: {patched_image_through_msa_block.shape}")
Input shape of MSA block: torch.Size([1, 197, 768]) Output shape MSA block: torch.Size([1, 197, 768])
注意到当数据通过MSA块时,输入和输出的形状保持不变。
这并不意味着数据在通过时没有变化。
你可以尝试打印输入和输出张量,看看它是如何变化的(尽管这种变化会跨越 1 * 197 * 768 个值,可能难以直观展示)。
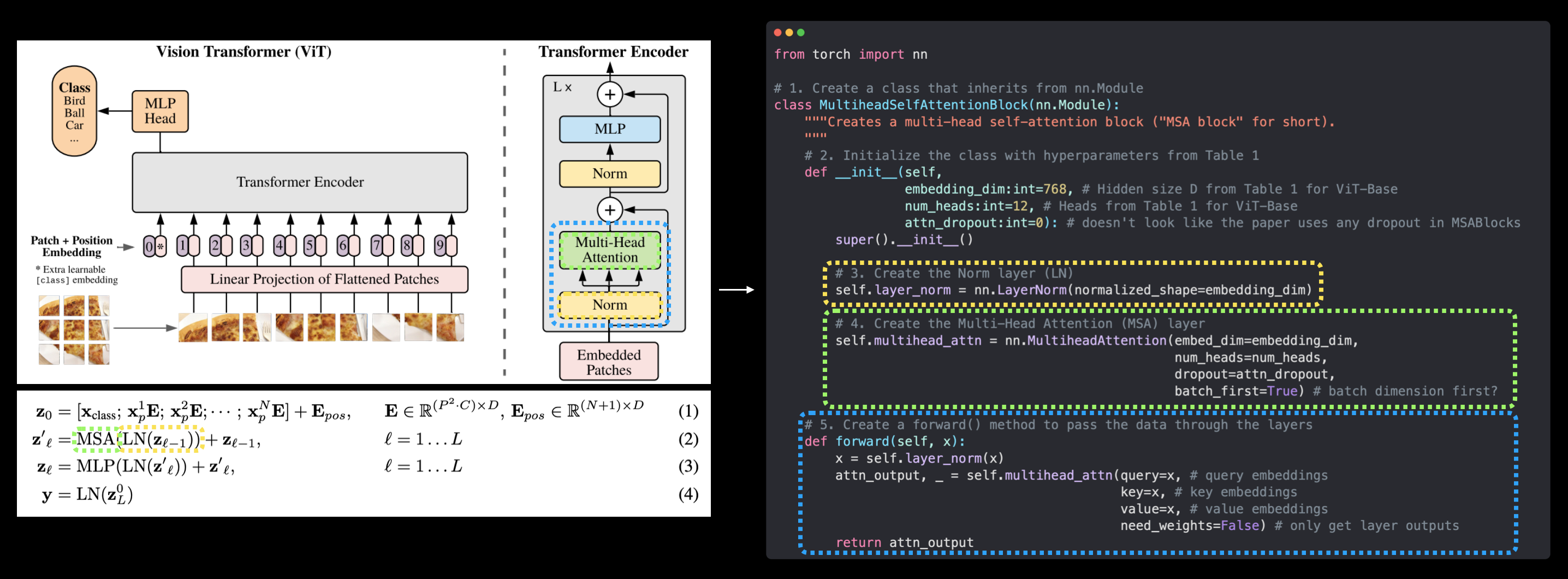
***左图:** 图1中的Vision Transformer架构,高亮显示了多头注意力和LayerNorm层,这些层构成了论文第3.1节中的公式2。右图: 使用PyTorch层复制公式2(不包括最后的跳跃连接)。*
我们现在正式复制了公式2(除了最后的残差连接,我们将在第7.1节中讨论)!
继续下一个!
6. 公式 3:多层感知机(MLP)¶
我们进展顺利!
让我们继续前进,重现公式 3:
$$ \begin{aligned} \mathbf{z}_{\ell} &=\operatorname{MLP}\left(\operatorname{LN}\left(\mathbf{z}_{\ell}^{\prime}\right)\right)+\mathbf{z}_{\ell}^{\prime}, & & \ell=1 \ldots L \end{aligned} $$
这里 MLP 代表“多层感知机”,LN 代表“层归一化”(如上所述)。
末尾的加法是跳跃/残差连接。
我们将公式 3 称为 Transformer 编码器的“MLP 块”(注意我们如何继续将架构分解为更小的部分)。

***左:** ViT 论文中的图 1,突出显示了 Transformer 编码器块中的 MLP 和归一化层以及残差连接(+)。 右: 将多层感知机(MLP)层、归一化层(LN)和残差连接映射到 ViT 论文中公式 3 的相应部分。*
6.1 MLP层¶
MLP(多层感知器)这个术语非常宽泛,因为它几乎可以指代任何形式的多层组合(因此得名“多层感知器”)。
但一般来说,它的结构遵循以下模式:
线性层 -> 非线性层 -> 线性层 -> 非线性层
在ViT论文中,MLP结构在3.1节中定义:
MLP包含两个层,并具有GELU非线性激活函数。
这里的“两个层”指的是线性层(在PyTorch中为torch.nn.Linear()),而“GELU非线性激活函数”是GELU(高斯误差线性单元)非线性激活函数(在PyTorch中为torch.nn.GELU())。
注意: 线性层(
torch.nn.Linear())有时也被称为“全连接层”或“前馈层”。某些论文甚至使用这三种术语来描述同一事物(如ViT论文中所示)。
关于MLP块的另一个细节直到附录B.1(训练)中才出现:
表3总结了我们不同模型的训练设置。...当使用Dropout时,它被应用于每个全连接层之后,除了qkv投影层和直接在添加位置嵌入到补丁嵌入之后。
这意味着MLP块中的每个线性层(或全连接层)都有一个Dropout层(在PyTorch中为torch.nn.Dropout())。
其值可以在ViT论文的表3中找到(对于ViT-Base,dropout=0.1)。
了解这些信息后,我们的MLP块结构将是:
层归一化 -> 线性层 -> 非线性层 -> Dropout -> 线性层 -> Dropout
线性层的超参数值可从表1中获取(MLP大小是线性层之间的隐藏单元数,隐藏大小$D$是MLP块的输出大小)。
6.2 使用PyTorch层复制公式3¶
让我们将在公式3中讨论的关于LayerNorm(LN)和MLP(MSA)层的所有内容付诸实践。
为此,我们将:
- 创建一个名为
MLPBlock的类,继承自torch.nn.Module。 - 使用ViT-Base模型的ViT论文中表1和表3的超参数初始化该类。
- 使用
torch.nn.LayerNorm()创建一个层归一化(LN)层,其normalized_shape参数与我们的嵌入维度(表1中的$D$)相同。 - 使用
torch.nn.Linear()、torch.nn.Dropout()和torch.nn.GELU()创建一系列MLP层,并使用表1和表3中的适当超参数值。 - 为我们的类创建一个
forward()方法,通过LN层和MLP层传递输入。
# 1. Create a class that inherits from nn.Module
class MLPBlock(nn.Module):
"""Creates a layer normalized multilayer perceptron block ("MLP block" for short)."""
# 2. Initialize the class with hyperparameters from Table 1 and Table 3
def __init__(self,
embedding_dim:int=768, # Hidden Size D from Table 1 for ViT-Base
mlp_size:int=3072, # MLP size from Table 1 for ViT-Base
dropout:float=0.1): # Dropout from Table 3 for ViT-Base
super().__init__()
# 3. Create the Norm layer (LN)
self.layer_norm = nn.LayerNorm(normalized_shape=embedding_dim)
# 4. Create the Multilayer perceptron (MLP) layer(s)
self.mlp = nn.Sequential(
nn.Linear(in_features=embedding_dim,
out_features=mlp_size),
nn.GELU(), # "The MLP contains two layers with a GELU non-linearity (section 3.1)."
nn.Dropout(p=dropout),
nn.Linear(in_features=mlp_size, # needs to take same in_features as out_features of layer above
out_features=embedding_dim), # take back to embedding_dim
nn.Dropout(p=dropout) # "Dropout, when used, is applied after every dense layer.."
)
# 5. Create a forward() method to pass the data throguh the layers
def forward(self, x):
x = self.layer_norm(x)
x = self.mlp(x)
return x
注意: 与图1不同,我们的
MLPBlock()不包含跳跃连接或残差连接(方程3中的"$+\mathbf{z}_{\ell}^{\prime}$"),我们将在稍后创建整个Transformer编码器时加入这一部分。
MLPBlock 类已创建!
让我们尝试创建一个 MLPBlock 实例,并通过我们在第5.3节中创建的 patched_image_through_msa_block 变量来测试它。
# Create an instance of MLPBlock
mlp_block = MLPBlock(embedding_dim=768, # from Table 1
mlp_size=3072, # from Table 1
dropout=0.1) # from Table 3
# Pass output of MSABlock through MLPBlock
patched_image_through_mlp_block = mlp_block(patched_image_through_msa_block)
print(f"Input shape of MLP block: {patched_image_through_msa_block.shape}")
print(f"Output shape MLP block: {patched_image_through_mlp_block.shape}")
Input shape of MLP block: torch.Size([1, 197, 768]) Output shape MLP block: torch.Size([1, 197, 768])
请注意,当数据进入和离开MLP块时,其输入和输出形状再次保持不变。
然而,当数据通过MLP块内部的nn.Linear()层时,形状确实会发生变化(从表1中的MLP大小扩展,然后压缩回表1中的隐藏大小$D$)。
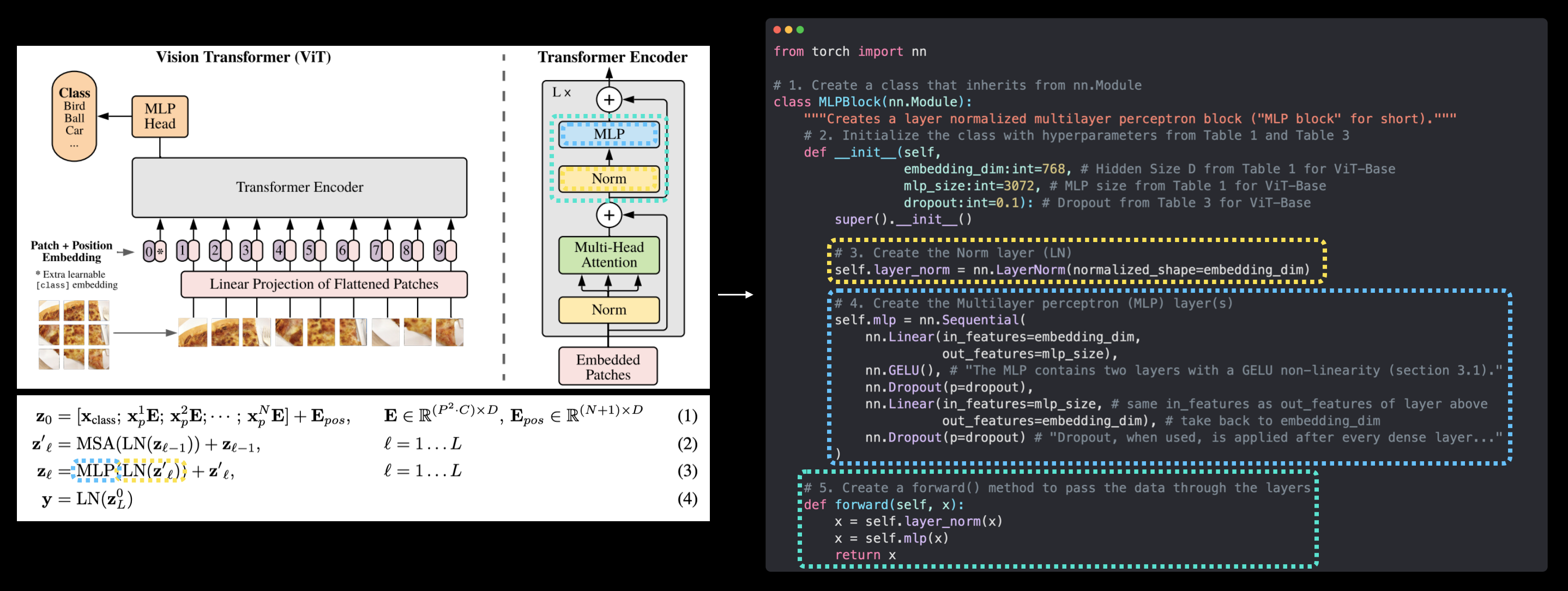
左:图1中的Vision Transformer架构,其中MLP和Norm层高亮显示,这些层构成了论文第3.1节中的方程3。右:使用PyTorch层复制方程3(不包括末端的跳跃连接)。
呵呵!
方程3已复制(除了末端的残差连接,我们将在第7.1节讨论这一点)!
现在我们已经将方程2和3转换为PyTorch代码,接下来让我们将它们结合起来,创建Transformer编码器。
7. 创建Transformer编码器¶
现在是时候将我们的MultiheadSelfAttentionBlock(方程2)和MLPBlock(方程3)堆叠在一起,创建ViT架构中的Transformer编码器了。
在深度学习中,"编码器"或"自动编码器"通常指的是一系列层,用于"编码"输入(将其转换为某种形式的数值表示)。
在我们的例子中,Transformer编码器将使用一系列交替的MSA块和MLP块,根据ViT论文第3.1节所述,将我们的分块图像嵌入编码为学习到的表示:
Transformer编码器(Vaswani等人,2017)由交替的多头自注意力(MSA,见附录A)和MLP块(方程2、3)组成。在每个块之前应用层归一化(LN),并且在每个块之后应用残差连接(Wang等人,2019;Baevski & Auli,2019)。
我们已经创建了MSA和MLP块,但残差连接呢?
残差连接(也称为跳跃连接),首次在论文《用于图像识别的深度残差学习》中提出,通过将其输入与其后续输出相加来实现。
后续输出可能是一个或多个层之后的结果。
在ViT架构中,残差连接意味着MSA块的输入在传递到MLP块之前被加回到MSA块的输出。
MLP块在传递到下一个Transformer编码器块之前也会发生同样的情况。
或者用伪代码表示:
x_input -> MSA_block -> [MSA_block_output + x_input] -> MLP_block -> [MLP_block_output + MSA_block_output + x_input] -> ...
这样做有什么作用?
残差连接的主要思想之一是防止权重值和梯度更新变得过小,从而允许更深的网络,进而允许学习更深的表示。
注意: 标志性的计算机视觉架构"ResNet"之所以如此命名,是因为引入了残差连接。你可以在
torchvision.models中找到许多预训练的ResNet架构版本。
7.1 通过组合我们自定义的层来创建一个Transformer编码器¶
说够了,让我们看看实际操作,通过组合我们之前创建的层来使用PyTorch制作一个ViT Transformer编码器。
为此,我们将:
- 创建一个名为
TransformerEncoderBlock的类,继承自torch.nn.Module。 - 使用ViT-Base模型的ViT论文中表1和表3的 hyperparameters 初始化该类。
- 使用我们第5.2节中的
MultiheadSelfAttentionBlock,以适当的参数实例化一个用于公式2的MSA块。 - 使用我们第6.2节中的
MLPBlock,以适当的参数实例化一个用于公式3的MLP块。 - 为我们的
TransformerEncoderBlock类创建一个forward()方法。 - 为MSA块(用于公式2)创建一个残差连接。
- 为MLP块(用于公式3)创建一个残差连接。
# 1. Create a class that inherits from nn.Module
class TransformerEncoderBlock(nn.Module):
"""Creates a Transformer Encoder block."""
# 2. Initialize the class with hyperparameters from Table 1 and Table 3
def __init__(self,
embedding_dim:int=768, # Hidden size D from Table 1 for ViT-Base
num_heads:int=12, # Heads from Table 1 for ViT-Base
mlp_size:int=3072, # MLP size from Table 1 for ViT-Base
mlp_dropout:float=0.1, # Amount of dropout for dense layers from Table 3 for ViT-Base
attn_dropout:float=0): # Amount of dropout for attention layers
super().__init__()
# 3. Create MSA block (equation 2)
self.msa_block = MultiheadSelfAttentionBlock(embedding_dim=embedding_dim,
num_heads=num_heads,
attn_dropout=attn_dropout)
# 4. Create MLP block (equation 3)
self.mlp_block = MLPBlock(embedding_dim=embedding_dim,
mlp_size=mlp_size,
dropout=mlp_dropout)
# 5. Create a forward() method
def forward(self, x):
# 6. Create residual connection for MSA block (add the input to the output)
x = self.msa_block(x) + x
# 7. Create residual connection for MLP block (add the input to the output)
x = self.mlp_block(x) + x
return x
太棒了!
Transformer Encoder 模块创建成功!

***左侧:** 来自 ViT 论文的图 1,其中 ViT 架构的 Transformer Encoder 部分被高亮显示。 右侧: Transformer Encoder 对应 ViT 论文中的公式 2 和公式 3,Transformer Encoder 由交替的公式 2(多头注意力)和公式 3(多层感知机)组成。*
看看我们是如何像搭积木一样,一步一步地将整个架构拼凑起来的,一次编码一个“砖块”(或公式)。

将 ViT 的 Transformer Encoder 映射到代码。
你可能注意到 ViT 论文中的表 1 有一个 Layers 列。这指的是特定 ViT 架构中 Transformer Encoder 块的数量。
在我们的例子中,对于 ViT-Base,我们将堆叠 12 个这样的 Transformer Encoder 块来构成我们架构的主干(我们将在第 8 节中详细讨论)。
让我们用 torchinfo.summary() 来查看将形状为 (1, 197, 768) -> (batch_size, num_patches, embedding_dimension) 的输入传递给我们的 Transformer Encoder 块的概要。
# Create an instance of TransformerEncoderBlock
transformer_encoder_block = TransformerEncoderBlock()
# # Print an input and output summary of our Transformer Encoder (uncomment for full output)
# summary(model=transformer_encoder_block,
# input_size=(1, 197, 768), # (batch_size, num_patches, embedding_dimension)
# col_names=["input_size", "output_size", "num_params", "trainable"],
# col_width=20,
# row_settings=["var_names"])
哇!看看这些参数!
你可以看到我们的输入在通过Transformer编码器块中的MSA块和MLP块的所有不同层时,形状发生了变化,最后在末端恢复到原来的形状。
注意: 尽管输入到Transformer编码器块的形状在块的输出处相同,但这并不意味着这些值没有被处理。Transformer编码器块(以及将它们堆叠在一起)的整个目标是通过中间的各种层来学习输入的深层表示。
7.2 使用PyTorch的Transformer层创建Transformer编码器¶
到目前为止,我们已经自己构建了Transformer编码器层的各个组件及其本身。
但由于Transformer的流行和有效性,PyTorch现在内置了Transformer层作为torch.nn的一部分。
例如,我们可以使用torch.nn.TransformerEncoderLayer()重新创建我们刚刚创建的TransformerEncoderBlock,并设置与上述相同的超参数。
# Create the same as above with torch.nn.TransformerEncoderLayer()
torch_transformer_encoder_layer = nn.TransformerEncoderLayer(d_model=768, # Hidden size D from Table 1 for ViT-Base
nhead=12, # Heads from Table 1 for ViT-Base
dim_feedforward=3072, # MLP size from Table 1 for ViT-Base
dropout=0.1, # Amount of dropout for dense layers from Table 3 for ViT-Base
activation="gelu", # GELU non-linear activation
batch_first=True, # Do our batches come first?
norm_first=True) # Normalize first or after MSA/MLP layers?
torch_transformer_encoder_layer
TransformerEncoderLayer(
(self_attn): MultiheadAttention(
(out_proj): NonDynamicallyQuantizableLinear(in_features=768, out_features=768, bias=True)
)
(linear1): Linear(in_features=768, out_features=3072, bias=True)
(dropout): Dropout(p=0.1, inplace=False)
(linear2): Linear(in_features=3072, out_features=768, bias=True)
(norm1): LayerNorm((768,), eps=1e-05, elementwise_affine=True)
(norm2): LayerNorm((768,), eps=1e-05, elementwise_affine=True)
(dropout1): Dropout(p=0.1, inplace=False)
(dropout2): Dropout(p=0.1, inplace=False)
)
为了进一步检查,让我们用 torchinfo.summary() 获取一个摘要。
# # Get the output of PyTorch's version of the Transformer Encoder (uncomment for full output)
# summary(model=torch_transformer_encoder_layer,
# input_size=(1, 197, 768), # (batch_size, num_patches, embedding_dimension)
# col_names=["input_size", "output_size", "num_params", "trainable"],
# col_width=20,
# row_settings=["var_names"])

由于 torch.nn.TransformerEncoderLayer() 构建层的方式不同,输出的总结与我们略有不同。
但它使用的层、参数数量以及输入和输出形状是相同的。
你可能会想:“既然我们可以用 PyTorch 层这么快地创建 Transformer Encoder,为什么还要费心重现方程 2 和 3 呢?”
答案是:练习。
现在我们已经从一篇论文中复制了一系列方程和层,如果你需要改变层并尝试不同的东西,你可以做到。
但使用 PyTorch 预构建层的优点包括:
- 更不容易出错 - 通常,如果一个层被纳入 PyTorch 标准库,它已经过测试并被证明是有效的。
- 潜在的更好性能 - 截至 2022 年 7 月和 PyTorch 1.12,PyTorch 实现的
torch.nn.TransformerEncoderLayer()在许多常见工作负载上可以看到 超过 2 倍的加速。
最后,由于 ViT 架构在完整的架构中使用了多个 Transformer 层堆叠在一起(表 1 显示了 ViT-Base 情况下有 12 层),你可以使用 torch.nn.TransformerEncoder(encoder_layer, num_layers) 来实现,其中:
encoder_layer- 使用torch.nn.TransformerEncoderLayer()创建的目标 Transformer Encoder 层。num_layers- 要堆叠在一起的 Transformer Encoder 层数。
8. 综合所有部分创建 ViT¶
好了,好了,好了,我们已经走了很长的路!
但现在是要做激动人心的事情的时候了,把所有的拼图碎片拼在一起。
我们将结合我们创建的所有模块来复制完整的 ViT 架构。
从分块和位置嵌入到 Transformer 编码器再到 MLP 头部。
但是等等,我们还没有创建方程 4...
$$ \begin{aligned} \mathbf{y} &=\operatorname{LN}\left(\mathbf{z}_{L}^{0}\right) & & \end{aligned} $$
别担心,我们可以把方程 4 放到我们的整体 ViT 架构类中。
我们只需要一个 torch.nn.LayerNorm() 层和一个 torch.nn.Linear() 层,将 Transformer 编码器逻辑输出的第 0 个索引 ($\mathbf{z}_{L}^{0}$) 转换为我们拥有的目标类别数。
为了创建完整的架构,我们还需要将多个 TransformerEncoderBlock 堆叠在一起,我们可以通过将它们传递给 torch.nn.Sequential() 来实现(这将创建一系列的 TransformerEncoderBlock)。
我们将关注表 1 中的 ViT-Base 超参数,但我们的代码应该适用于其他 ViT 变体。
创建 ViT 将是我们迄今为止最大的代码块,但我们能做到!
最后,为了让我们的 ViT 实现活起来,让我们:
- 创建一个名为
ViT的类,继承自torch.nn.Module。 - 使用 ViT 论文中表 1 和表 3 的超参数初始化类,用于 ViT-Base 模型。
- 确保图像大小能被分块大小整除(图像应被分割成均匀的分块)。
- 使用公式 $N=H W / P^{2}$ 计算分块数量,其中 $H$ 是图像高度,$W$ 是图像宽度,$P$ 是分块大小。
- 创建一个可学习的类别嵌入令牌(方程 1),如上文第 4.6 节所述。
- 创建一个可学习的位置嵌入向量(方程 1),如上文第 4.7 节所述。
- 设置嵌入丢弃层,如 ViT 论文附录 B.1 所述。
- 使用第 4.5 节中的
PatchEmbedding类创建分块嵌入层。 - 通过将第 7.1 节中创建的
TransformerEncoderBlock列表传递给torch.nn.Sequential()来创建一系列 Transformer 编码器块(方程 2 和 3)。 - 通过传递一个
torch.nn.LayerNorm()(LN)层和一个torch.nn.Linear(out_features=num_classes)层(其中num_classes是目标类别数)到torch.nn.Sequential()来创建 MLP 头部(也称为分类器头部或方程 4)。 - 创建一个接受输入的
forward()方法。 - 获取输入的批次大小(形状的第一个维度)。
- 使用第 8 步创建的层创建分块嵌入(方程 1)。
- 使用第 5 步创建的层创建类别令牌嵌入,并使用
torch.Tensor.expand()在第 11 步找到的批次数量上扩展它(方程 1)。 - 使用
torch.cat()将第 13 步创建的类别令牌嵌入连接到第 12 步创建的分块嵌入的第一个维度(方程 1)。 - 将第 6 步创建的位置嵌入添加到第 14 步创建的分块和类别令牌嵌入(方程 1)。
- 将第 16 步创建的分块和位置嵌入通过第 7 步创建的丢弃层。
- 将第 16 步创建的分块和位置嵌入通过第 9 步创建的 Transformer 编码器层堆栈(方程 2 和 3)。
- 将第 17 步 Transformer 编码器层堆栈输出的第 0 个索引通过第 10 步创建的分类器头部(方程 4)。
- 跳舞并高呼 woohoo!!! 我们刚刚构建了一个视觉 Transformer!
准备好了吗?
让我们开始吧。
# 1. Create a ViT class that inherits from nn.Module
class ViT(nn.Module):
"""Creates a Vision Transformer architecture with ViT-Base hyperparameters by default."""
# 2. Initialize the class with hyperparameters from Table 1 and Table 3
def __init__(self,
img_size:int=224, # Training resolution from Table 3 in ViT paper
in_channels:int=3, # Number of channels in input image
patch_size:int=16, # Patch size
num_transformer_layers:int=12, # Layers from Table 1 for ViT-Base
embedding_dim:int=768, # Hidden size D from Table 1 for ViT-Base
mlp_size:int=3072, # MLP size from Table 1 for ViT-Base
num_heads:int=12, # Heads from Table 1 for ViT-Base
attn_dropout:float=0, # Dropout for attention projection
mlp_dropout:float=0.1, # Dropout for dense/MLP layers
embedding_dropout:float=0.1, # Dropout for patch and position embeddings
num_classes:int=1000): # Default for ImageNet but can customize this
super().__init__() # don't forget the super().__init__()!
# 3. Make the image size is divisble by the patch size
assert img_size % patch_size == 0, f"Image size must be divisible by patch size, image size: {img_size}, patch size: {patch_size}."
# 4. Calculate number of patches (height * width/patch^2)
self.num_patches = (img_size * img_size) // patch_size**2
# 5. Create learnable class embedding (needs to go at front of sequence of patch embeddings)
self.class_embedding = nn.Parameter(data=torch.randn(1, 1, embedding_dim),
requires_grad=True)
# 6. Create learnable position embedding
self.position_embedding = nn.Parameter(data=torch.randn(1, self.num_patches+1, embedding_dim),
requires_grad=True)
# 7. Create embedding dropout value
self.embedding_dropout = nn.Dropout(p=embedding_dropout)
# 8. Create patch embedding layer
self.patch_embedding = PatchEmbedding(in_channels=in_channels,
patch_size=patch_size,
embedding_dim=embedding_dim)
# 9. Create Transformer Encoder blocks (we can stack Transformer Encoder blocks using nn.Sequential())
# Note: The "*" means "all"
self.transformer_encoder = nn.Sequential(*[TransformerEncoderBlock(embedding_dim=embedding_dim,
num_heads=num_heads,
mlp_size=mlp_size,
mlp_dropout=mlp_dropout) for _ in range(num_transformer_layers)])
# 10. Create classifier head
self.classifier = nn.Sequential(
nn.LayerNorm(normalized_shape=embedding_dim),
nn.Linear(in_features=embedding_dim,
out_features=num_classes)
)
# 11. Create a forward() method
def forward(self, x):
# 12. Get batch size
batch_size = x.shape[0]
# 13. Create class token embedding and expand it to match the batch size (equation 1)
class_token = self.class_embedding.expand(batch_size, -1, -1) # "-1" means to infer the dimension (try this line on its own)
# 14. Create patch embedding (equation 1)
x = self.patch_embedding(x)
# 15. Concat class embedding and patch embedding (equation 1)
x = torch.cat((class_token, x), dim=1)
# 16. Add position embedding to patch embedding (equation 1)
x = self.position_embedding + x
# 17. Run embedding dropout (Appendix B.1)
x = self.embedding_dropout(x)
# 18. Pass patch, position and class embedding through transformer encoder layers (equations 2 & 3)
x = self.transformer_encoder(x)
# 19. Put 0 index logit through classifier (equation 4)
x = self.classifier(x[:, 0]) # run on each sample in a batch at 0 index
return x
- 🕺💃🥳 哇呼!我们刚刚构建了一个视觉变换器!
真是费了不少功夫!
我们一步步地创建了层和块,输入和输出,并将它们全部组合在一起,构建了我们自己的ViT!
让我们快速创建一个演示,展示类标记嵌入在批次维度上的扩展情况。
# Example of creating the class embedding and expanding over a batch dimension
batch_size = 32
class_token_embedding_single = nn.Parameter(data=torch.randn(1, 1, 768)) # create a single learnable class token
class_token_embedding_expanded = class_token_embedding_single.expand(batch_size, -1, -1) # expand the single learnable class token across the batch dimension, "-1" means to "infer the dimension"
# Print out the change in shapes
print(f"Shape of class token embedding single: {class_token_embedding_single.shape}")
print(f"Shape of class token embedding expanded: {class_token_embedding_expanded.shape}")
Shape of class token embedding single: torch.Size([1, 1, 768]) Shape of class token embedding expanded: torch.Size([32, 1, 768])
注意第一个维度是如何扩展到批量大小的,而其他维度保持不变(因为它们是通过 .expand(batch_size, -1, -1) 中的 "-1" 维度推断出来的)。
好了,是时候测试一下 ViT() 类了。
让我们创建一个与单张图像形状相同的随机张量,传递给 ViT 的一个实例,看看会发生什么。
set_seeds()
# Create a random tensor with same shape as a single image
random_image_tensor = torch.randn(1, 3, 224, 224) # (batch_size, color_channels, height, width)
# Create an instance of ViT with the number of classes we're working with (pizza, steak, sushi)
vit = ViT(num_classes=len(class_names))
# Pass the random image tensor to our ViT instance
vit(random_image_tensor)
tensor([[-0.2377, 0.7360, 1.2137]], grad_fn=<AddmmBackward0>)
太棒了!
看来我们的随机图像张量已经顺利通过了ViT架构,并输出了三个对数(每个类别一个)。
而且由于我们的ViT类有许多可定制的参数,如果我们愿意,可以调整img_size、patch_size或num_classes。
8.1 获取ViT模型的可视化摘要¶
我们手工打造了自己的ViT架构版本,并且已经看到随机图像张量可以完全流经该模型。
那么,我们是否可以使用 torchinfo.summary() 来获取模型中所有层的输入和输出形状的可视化概览呢?
注意: ViT论文中提到使用4096的批量大小进行训练,然而,这需要相当大的CPU/GPU计算内存来处理(批量越大,所需的内存越多)。因此,为了避免内存错误,我们将坚持使用32的批量大小。如果你有更多内存的硬件访问权限,你可以随时增加这个值。
from torchinfo import summary
# # Print a summary of our custom ViT model using torchinfo (uncomment for actual output)
# summary(model=vit,
# input_size=(32, 3, 224, 224), # (batch_size, color_channels, height, width)
# # col_names=["input_size"], # uncomment for smaller output
# col_names=["input_size", "output_size", "num_params", "trainable"],
# col_width=20,
# row_settings=["var_names"]
# )
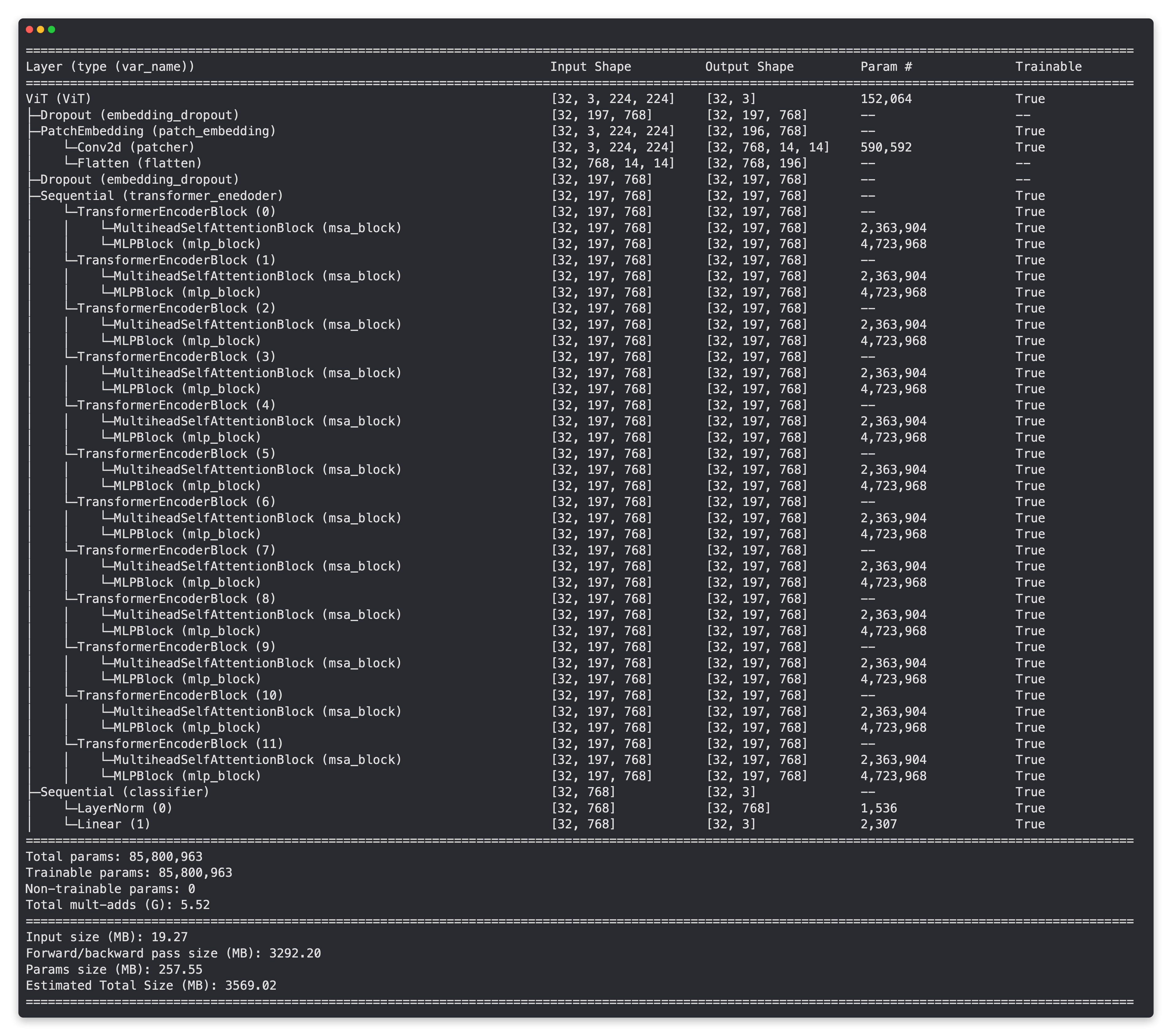
现在这些看起来真是不错的层!
也来看看总的参数数量,85,800,963,这是我们迄今为止最大的模型!
这个数字非常接近PyTorch预训练的ViT-Base模型(patch大小为16)在torch.vision.models.vit_b_16()中的86,567,656个总参数(尽管这些参数是针对ImageNet中的1000个类别)。
练习: 尝试将我们的
ViT()模型的num_classes参数改为1000,然后使用torchinfo.summary()创建另一个总结,看看我们的代码和torchvision.models.vit_b_16()之间的参数数量是否一致。
9. 为我们的 ViT 模型设置训练代码¶
好了,现在是简单部分。
训练!
为什么简单?
因为我们已经准备好了大部分所需内容,从我们的模型(vit)到我们的 DataLoader(train_dataloader、test_dataloader),再到我们在 05. PyTorch Going Modular 第 4 节 中创建的训练函数。
为了训练我们的模型,我们可以从 going_modular.going_modular.engine 导入 train() 函数。
我们需要的只是一个损失函数和一个优化器。
9.1 创建优化器¶
在 ViT 论文中搜索 "optimizer",第 4.1 节关于训练与微调的内容如下:
训练与微调。 我们使用 Adam 优化器(Kingma & Ba, 2015)训练所有模型,包括 ResNets,设置 $\beta_{1}=0.9, \beta_{2}=0.999$,批量大小为 4096,并应用高权重衰减 $0.1$,我们发现这对于所有模型的迁移学习非常有用(附录 D.1 表明,与常见做法相反,在我们的设置中,Adam 略优于 SGD 用于 ResNets)。
由此可见,他们选择使用 "Adam" 优化器(torch.optim.Adam())而不是 SGD(随机梯度下降,torch.optim.SGD())。
作者将 Adam 的 $\beta$ 值设置为 $\beta_{1}=0.9, \beta_{2}=0.999$,这些是 torch.optim.Adam(betas=(0.9, 0.999)) 中 betas 参数的默认值。
他们还提到了使用权重衰减(在优化过程中逐渐减小权重值以防止过拟合),我们可以通过 torch.optim.Adam(weight_decay=0.3) 中的 weight_decay 参数来设置(根据 ViT-* 在 ImageNet-1k 上的训练设置)。
我们将根据表 3 将优化器的学习率设置为 0.003(根据 ViT-* 在 ImageNet-1k 上的训练设置)。
正如之前讨论的,由于硬件限制,我们将使用小于 4096 的批量大小(如果你有大型 GPU,可以随意增加这个值)。
9.2 创建损失函数¶
奇怪的是,在 ViT 论文中搜索 "loss"、"loss function" 或 "criterion" 都没有结果。
然而,由于我们处理的目标问题是多类别分类(与 ViT 论文相同),我们将使用 torch.nn.CrossEntropyLoss()。
9.3 训练我们的 ViT 模型¶
好了,现在我们知道将要使用什么优化器和损失函数了,让我们设置训练代码来训练我们的 ViT 模型。
我们将首先从 going_modular.going_modular 导入 engine.py 脚本,然后设置优化器和损失函数,最后我们将使用 engine.py 中的 train() 函数来训练我们的 ViT 模型 10 个周期(我们使用的周期数比 ViT 论文中的少,以确保一切正常工作)。
from going_modular.going_modular import engine
# Setup the optimizer to optimize our ViT model parameters using hyperparameters from the ViT paper
optimizer = torch.optim.Adam(params=vit.parameters(),
lr=3e-3, # Base LR from Table 3 for ViT-* ImageNet-1k
betas=(0.9, 0.999), # default values but also mentioned in ViT paper section 4.1 (Training & Fine-tuning)
weight_decay=0.3) # from the ViT paper section 4.1 (Training & Fine-tuning) and Table 3 for ViT-* ImageNet-1k
# Setup the loss function for multi-class classification
loss_fn = torch.nn.CrossEntropyLoss()
# Set the seeds
set_seeds()
# Train the model and save the training results to a dictionary
results = engine.train(model=vit,
train_dataloader=train_dataloader,
test_dataloader=test_dataloader,
optimizer=optimizer,
loss_fn=loss_fn,
epochs=10,
device=device)
0%| | 0/10 [00:00<?, ?it/s]
Epoch: 1 | train_loss: 4.8759 | train_acc: 0.2891 | test_loss: 1.0465 | test_acc: 0.5417 Epoch: 2 | train_loss: 1.5900 | train_acc: 0.2617 | test_loss: 1.5876 | test_acc: 0.1979 Epoch: 3 | train_loss: 1.4644 | train_acc: 0.2617 | test_loss: 1.2738 | test_acc: 0.1979 Epoch: 4 | train_loss: 1.3159 | train_acc: 0.2773 | test_loss: 1.7498 | test_acc: 0.1979 Epoch: 5 | train_loss: 1.3114 | train_acc: 0.3008 | test_loss: 1.7444 | test_acc: 0.2604 Epoch: 6 | train_loss: 1.2445 | train_acc: 0.3008 | test_loss: 1.9704 | test_acc: 0.1979 Epoch: 7 | train_loss: 1.2050 | train_acc: 0.3984 | test_loss: 3.5480 | test_acc: 0.1979 Epoch: 8 | train_loss: 1.4368 | train_acc: 0.4258 | test_loss: 1.8324 | test_acc: 0.2604 Epoch: 9 | train_loss: 1.5757 | train_acc: 0.2344 | test_loss: 1.2848 | test_acc: 0.5417 Epoch: 10 | train_loss: 1.4658 | train_acc: 0.4023 | test_loss: 1.2389 | test_acc: 0.2604
太棒了!
我们的ViT模型终于活起来了!
不过,在我们披萨、牛排和寿司数据集上的表现似乎不太理想。
或许是因为我们遗漏了一些东西?
9.4 我们的训练设置缺少什么¶
原始的 ViT 架构在多个图像分类基准测试中取得了良好的结果(在发布时与许多最先进的结果相当或更好)。
然而,我们的结果(到目前为止)并不那么好。
有几个原因可能导致这种情况,但主要原因是规模。
原始 ViT 论文使用的数据量远大于我们的数据量(在深度学习中,更多的数据通常总是一件好事),并且训练周期更长(见表 3)。
| 超参数值 | ViT 论文 | 我们的实现 |
|---|---|---|
| 训练图像数量 | 1.3M(ImageNet-1k),14M(ImageNet-21k),303M(JFT) | 225 |
| 训练周期 | 7(最大数据集),90,300(ImageNet) | 10 |
| 批次大小 | 4096 | 32 |
| 学习率预热 | 10k 步(表 3) | 无 |
| 学习率衰减 | 线性/余弦(表 3) | 无 |
| 梯度裁剪 | 全局范数 1(表 3) | 无 |
尽管我们的 ViT 架构与论文相同,但 ViT 论文的结果是通过使用更多的数据和比我们更精细的训练方案实现的。
由于 ViT 架构的规模及其高数量的参数(增加学习能力),以及它使用的数据量(增加学习机会),ViT 论文训练方案中使用的许多技术,如学习率预热、学习率衰减和梯度裁剪,都是专门设计来防止过拟合(正则化)。
注意: 对于任何你不确定的技术,你通常可以通过搜索 "pytorch 技术名称" 快速找到示例,例如,如果你想了解学习率预热及其作用,你可以搜索 "pytorch learning rate warmup"。
好消息是,有许多使用大量数据预训练的 ViT 模型在线可用,我们将在第 10 节中看到一个实际应用。
9.5 绘制我们ViT模型的损失曲线¶
我们已经训练了ViT模型,并看到了页面上呈现的数字结果。
但现在让我们遵循数据探索者的座右铭:可视化,可视化,再可视化!
而对于模型来说,最好的可视化之一就是它的损失曲线。
要查看我们ViT模型的损失曲线,我们可以使用在04. PyTorch自定义数据集部分7.8中创建的helper_functions.py文件中的plot_loss_curves函数。
from helper_functions import plot_loss_curves
# Plot our ViT model's loss curves
plot_loss_curves(results)
嗯,看起来我们的模型的损失曲线波动很大。
至少损失看起来是在朝着正确的方向发展,但准确率曲线并没有显示出太多希望。
这些结果很可能是因为我们的ViT模型与ViT论文在数据资源和训练机制上的差异。
看来我们的模型严重欠拟合(未能达到我们期望的结果)。
我们是否可以考虑引入一个预训练的ViT模型来尝试解决这个问题?
10. 在同一数据集上使用 torchvision.models 中的预训练 ViT¶
我们在 06. PyTorch 迁移学习 中讨论了使用预训练模型的优势。
但由于我们现在已经从头开始训练了自己的 ViT,并且取得了不太理想的结果,因此迁移学习(使用预训练模型)的优点真正显现出来。
10.1 为什么要使用预训练模型?¶
许多现代机器学习研究论文的一个重要说明是,很多结果是通过大量数据集和庞大的计算资源获得的。
而在现代机器学习中,原始的完全训练好的 ViT 很可能不会被认为是一个“超级大型”的训练设置(模型不断变得越来越大)。
阅读 ViT 论文第 4.2 节:
最后,在公共 ImageNet-21k 数据集上预训练的 ViT-L/16 模型在大多数数据集上表现也很好,同时预训练所需的资源更少:它可以在大约 30 天内使用标准的云 TPUv3 8 核进行训练。
截至 2022 年 7 月,租用 TPUv3(Tensor Processing Unit 版本 3)在 Google Cloud 上的 8 核价格为每小时 8 美元。
连续租用 30 天的费用为 5,760 美元。
这种成本(金钱和时间)对于一些大型研究团队或企业可能是可行的,但对于许多人来说则不然。
因此,通过 torchvision.models、timm(Torch Image Models 库)、HuggingFace Hub 或甚至从论文作者本人那里获取预训练模型(机器学习研究人员发布其研究论文的代码和预训练模型的趋势正在增长,我非常喜欢这一趋势,这些资源可以在 Paperswithcode.com 上找到)。
如果你专注于利用特定模型架构的优势,而不是创建自定义架构,我强烈建议使用预训练模型。
10.2 获取预训练的 ViT 模型并创建特征提取器¶
我们可以从 torchvision.models 中获取预训练的 ViT 模型。
我们将从头开始,首先确保我们安装了正确版本的 torch 和 torchvision。
注意: 以下代码需要
torchv0.12+ 和torchvisionv0.13+ 才能使用最新的torchvision模型权重 API。
# The following requires torch v0.12+ and torchvision v0.13+
import torch
import torchvision
print(torch.__version__)
print(torchvision.__version__)
1.12.0+cu102 0.13.0+cu102
接下来,我们将设置设备无关的代码。
device = "cuda" if torch.cuda.is_available() else "cpu"
device
'cuda'
最后,我们将从 torchvision.models 中获取预训练的 ViT-Base(补丁大小为16),并将其准备为特征提取器迁移学习模型,以适应我们的 FoodVision Mini 用例。
具体来说,我们将:
- 从
torchvision.models.ViT_B_16_Weights.DEFAULT获取在 ImageNet-1k 上训练的 ViT-Base 的预训练权重(DEFAULT表示最佳可用权重)。 - 通过
torchvision.models.vit_b_16设置一个 ViT 模型实例,传递步骤1中的预训练权重,并将其发送到目标设备。 - 通过将步骤2中创建的基础 ViT 模型的所有参数的
requires_grad属性设置为False,冻结所有参数。 - 更新步骤2中创建的 ViT 模型的分类器头,以适应我们自己的问题,将
out_features的数量更改为我们的类别数(披萨、牛排、寿司)。
我们在 06. PyTorch 迁移学习 的 3.2 节:设置预训练模型 和 3.4 节:冻结基础模型并更改输出层以适应我们的需求 中介绍了类似的步骤。
# 1. Get pretrained weights for ViT-Base
pretrained_vit_weights = torchvision.models.ViT_B_16_Weights.DEFAULT # requires torchvision >= 0.13, "DEFAULT" means best available
# 2. Setup a ViT model instance with pretrained weights
pretrained_vit = torchvision.models.vit_b_16(weights=pretrained_vit_weights).to(device)
# 3. Freeze the base parameters
for parameter in pretrained_vit.parameters():
parameter.requires_grad = False
# 4. Change the classifier head (set the seeds to ensure same initialization with linear head)
set_seeds()
pretrained_vit.heads = nn.Linear(in_features=768, out_features=len(class_names)).to(device)
# pretrained_vit # uncomment for model output
预训练的 ViT 特征提取器模型已创建!
现在让我们通过打印 torchinfo.summary() 来查看一下。
# # Print a summary using torchinfo (uncomment for actual output)
# summary(model=pretrained_vit,
# input_size=(32, 3, 224, 224), # (batch_size, color_channels, height, width)
# # col_names=["input_size"], # uncomment for smaller output
# col_names=["input_size", "output_size", "num_params", "trainable"],
# col_width=20,
# row_settings=["var_names"]
# )
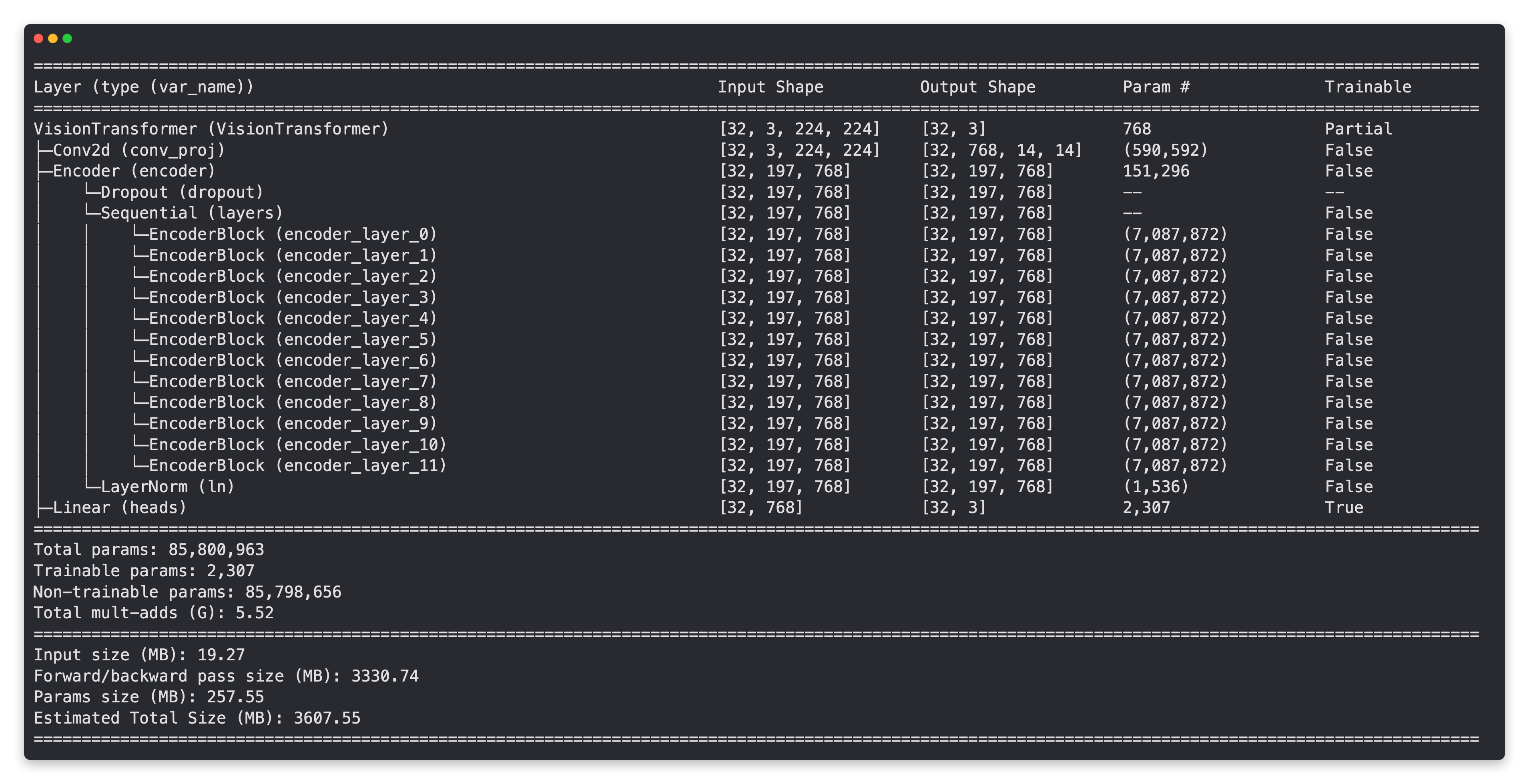
太棒了!
注意,只有输出层是可训练的,而其余所有层都是不可训练的(冻结的)。
并且,总参数数量85,800,963与我们在上面自定义的ViT模型相同。
但pretrained_vit的可训练参数数量远远低于我们自定义的vit,仅有2,307个,而自定义的vit有85,800,963个(在我们自定义的vit中,由于我们从头开始训练,所有参数都是可训练的)。
这意味着预训练模型应该会训练得更快,我们甚至可能可以使用更大的批量大小,因为较少的参数更新会占用内存。
10.3 为预训练的ViT模型准备数据¶
我们在第2节中已经下载并创建了我们自己的ViT模型的DataLoader。
因此,我们不一定需要再次进行这一步骤。
但为了练习,让我们下载一些图像数据(为Food Vision Mini准备的披萨、牛排和寿司图像),设置训练和测试目录,然后将图像转换为张量和DataLoader。
我们可以从课程GitHub下载披萨、牛排和寿司图像,并使用我们在07. PyTorch实验跟踪 第1节中创建的download_data()函数。
from helper_functions import download_data
# Download pizza, steak, sushi images from GitHub
image_path = download_data(source="https://github.com/mrdbourke/pytorch-deep-learning/raw/main/data/pizza_steak_sushi.zip",
destination="pizza_steak_sushi")
image_path
[INFO] data/pizza_steak_sushi directory exists, skipping download.
PosixPath('data/pizza_steak_sushi')
现在我们将设置训练和测试目录的路径。
# Setup train and test directory paths
train_dir = image_path / "train"
test_dir = image_path / "test"
train_dir, test_dir
(PosixPath('data/pizza_steak_sushi/train'),
PosixPath('data/pizza_steak_sushi/test'))
最后,我们将把图像转换为张量,并将这些张量转换为 DataLoader。
由于我们使用的是来自 torchvision.models 的预训练模型,因此可以调用其 transforms() 方法来获取所需的转换。
请记住,如果你打算使用预训练模型,通常重要的是确保你自己的自定义数据以与原始模型训练数据相同的方式进行转换/格式化。
我们在 06. PyTorch 迁移学习第 2.2 节 中介绍了这种“自动”创建转换的方法。
# Get automatic transforms from pretrained ViT weights
pretrained_vit_transforms = pretrained_vit_weights.transforms()
print(pretrained_vit_transforms)
ImageClassification(
crop_size=[224]
resize_size=[256]
mean=[0.485, 0.456, 0.406]
std=[0.229, 0.224, 0.225]
interpolation=InterpolationMode.BILINEAR
)
现在我们已经准备好了变换,可以使用我们在05. PyTorch Going Modular 第2节中创建的data_setup.create_dataloaders()方法将图像转换为DataLoaders。
由于我们使用的是特征提取模型(可训练参数较少),我们可以将批量大小增加到一个更高的值(如果我们将其设置为1024,我们将模仿在Better plain ViT baselines for ImageNet-1k一文中发现的改进,该文改进了原始ViT论文并建议额外阅读)。但由于我们总共只有约200个训练样本,我们将坚持使用32。
# Setup dataloaders
train_dataloader_pretrained, test_dataloader_pretrained, class_names = data_setup.create_dataloaders(train_dir=train_dir,
test_dir=test_dir,
transform=pretrained_vit_transforms,
batch_size=32) # Could increase if we had more samples, such as here: https://arxiv.org/abs/2205.01580 (there are other improvements there too...)
10.4 训练特征提取器 ViT 模型¶
特征提取器模型准备就绪,DataLoaders 也准备就绪,是时候开始训练了!
与之前一样,我们将使用 Adam 优化器(torch.optim.Adam()),学习率为 1e-3,并使用 torch.nn.CrossEntropyLoss() 作为损失函数。
我们在 05. PyTorch Going Modular 第 4 节 中创建的 engine.train() 函数将处理其余部分。
from going_modular.going_modular import engine
# Create optimizer and loss function
optimizer = torch.optim.Adam(params=pretrained_vit.parameters(),
lr=1e-3)
loss_fn = torch.nn.CrossEntropyLoss()
# Train the classifier head of the pretrained ViT feature extractor model
set_seeds()
pretrained_vit_results = engine.train(model=pretrained_vit,
train_dataloader=train_dataloader_pretrained,
test_dataloader=test_dataloader_pretrained,
optimizer=optimizer,
loss_fn=loss_fn,
epochs=10,
device=device)
0%| | 0/10 [00:00<?, ?it/s]
Epoch: 1 | train_loss: 0.7665 | train_acc: 0.7227 | test_loss: 0.5432 | test_acc: 0.8665 Epoch: 2 | train_loss: 0.3428 | train_acc: 0.9453 | test_loss: 0.3263 | test_acc: 0.8977 Epoch: 3 | train_loss: 0.2064 | train_acc: 0.9531 | test_loss: 0.2707 | test_acc: 0.9081 Epoch: 4 | train_loss: 0.1556 | train_acc: 0.9570 | test_loss: 0.2422 | test_acc: 0.9081 Epoch: 5 | train_loss: 0.1246 | train_acc: 0.9727 | test_loss: 0.2279 | test_acc: 0.8977 Epoch: 6 | train_loss: 0.1216 | train_acc: 0.9766 | test_loss: 0.2129 | test_acc: 0.9280 Epoch: 7 | train_loss: 0.0938 | train_acc: 0.9766 | test_loss: 0.2352 | test_acc: 0.8883 Epoch: 8 | train_loss: 0.0797 | train_acc: 0.9844 | test_loss: 0.2281 | test_acc: 0.8778 Epoch: 9 | train_loss: 0.1098 | train_acc: 0.9883 | test_loss: 0.2074 | test_acc: 0.9384 Epoch: 10 | train_loss: 0.0650 | train_acc: 0.9883 | test_loss: 0.1804 | test_acc: 0.9176
我的天!
看来我们预训练的 ViT 特征提取器表现远超我们从零开始训练的自定义 ViT 模型(在相同时间内)。
让我们直观地看看。
# Plot the loss curves
from helper_functions import plot_loss_curves
plot_loss_curves(pretrained_vit_results)
哇塞!
这些损失曲线看起来非常接近教科书上的理想曲线(真的很棒),你可以参考04. PyTorch 自定义数据集 第8节来了解理想的损失曲线应该是什么样子。
这就是迁移学习的威力!
我们用相同的模型架构取得了出色的结果,只不过我们的自定义实现是从头开始训练的(性能较差),而这个特征提取器模型背后有着来自ImageNet的预训练权重。
你觉得呢?
如果我们继续训练这个特征提取器模型,它的性能会进一步提升吗?
10.6 保存特征提取器ViT模型并检查文件大小¶
看来我们的ViT特征提取器模型在Food Vision Mini问题上表现相当不错。
或许我们可能想尝试将其部署到生产环境中,看看它在实际应用中的表现如何(在这种情况下,部署意味着将我们训练好的模型放入一个应用程序中,比如让用户使用智能手机拍摄食物照片,并查看我们的模型是否认为它是披萨、牛排或寿司)。
为此,我们可以首先使用我们在05. PyTorch Going Modular第5节中创建的utils.save_model()函数来保存我们的模型。
# Save the model
from going_modular.going_modular import utils
utils.save_model(model=pretrained_vit,
target_dir="models",
model_name="08_pretrained_vit_feature_extractor_pizza_steak_sushi.pth")
[INFO] Saving model to: models/08_pretrained_vit_feature_extractor_pizza_steak_sushi.pth
既然我们在考虑部署这个模型,了解它的大小(以兆字节或MB为单位)会很有帮助。
因为我们希望Food Vision Mini应用程序运行得快,通常一个性能良好但较小的模型会比一个性能极佳但较大的模型更优。
我们可以使用Python的pathlib.Path().stat()方法的st_size属性,同时传入我们模型的文件路径名,来检查模型的大小(以字节为单位)。
然后我们可以将字节大小转换为兆字节。
from pathlib import Path
# Get the model size in bytes then convert to megabytes
pretrained_vit_model_size = Path("models/08_pretrained_vit_feature_extractor_pizza_steak_sushi.pth").stat().st_size // (1024*1024) # division converts bytes to megabytes (roughly)
print(f"Pretrained ViT feature extractor model size: {pretrained_vit_model_size} MB")
Pretrained ViT feature extractor model size: 327 MB
嗯,看起来我们用于Food Vision Mini的ViT特征提取器模型大小约为327 MB。
这与07. PyTorch实验跟踪部分9中的EffNetB2特征提取器模型相比如何?
| 模型 | 模型大小 (MB) | 测试损失 | 测试准确度 |
|---|---|---|---|
| EffNetB2特征提取器^ | 29 | ~0.3906 | ~0.9384 |
| ViT特征提取器 | 327 | ~0.1084 | ~0.9384 |
注意: ^ 参考中的EffNetB2模型是使用20%的披萨、牛排和寿司数据(图片数量是ViT特征提取器训练数据的两倍)进行训练的,而ViT特征提取器则是使用10%的披萨、牛排和寿司数据进行训练的。一个练习是使用相同数量的数据(20%的披萨、牛排和寿司数据)训练ViT特征提取器模型,看看结果能提高多少。
EffNetB2模型的大小约为ViT模型的1/11,但测试损失和准确度结果相似。
然而,当使用相同数据(20%的披萨、牛排和寿司数据)进行训练时,ViT模型的结果可能会进一步提高。
但在部署方面,如果我们比较这两个模型,我们需要考虑的是,ViT模型额外提高的准确度是否值得模型大小增加约11倍?
也许这样一个大型模型加载/运行时间会更长,并且不会像性能相似但尺寸大幅减小的EffNetB2那样提供良好的体验。
11. 对自定义图像进行预测¶
最后,我们将进行终极测试,对我们的自定义数据进行预测。
让我们下载披萨爸爸的图像(一张我爸爸吃披萨的照片),并使用我们的ViT特征提取器对其进行预测。
为此,我们可以使用在06. PyTorch迁移学习第6节中创建的pred_and_plot()函数。为了方便起见,我将此函数保存到了课程GitHub上的going_modular.going_modular.predictions.py文件中。
import requests
# Import function to make predictions on images and plot them
from going_modular.going_modular.predictions import pred_and_plot_image
# Setup custom image path
custom_image_path = image_path / "04-pizza-dad.jpeg"
# Download the image if it doesn't already exist
if not custom_image_path.is_file():
with open(custom_image_path, "wb") as f:
# When downloading from GitHub, need to use the "raw" file link
request = requests.get("https://raw.githubusercontent.com/mrdbourke/pytorch-deep-learning/main/images/04-pizza-dad.jpeg")
print(f"Downloading {custom_image_path}...")
f.write(request.content)
else:
print(f"{custom_image_path} already exists, skipping download.")
# Predict on custom image
pred_and_plot_image(model=pretrained_vit,
image_path=custom_image_path,
class_names=class_names)
data/pizza_steak_sushi/04-pizza-dad.jpeg already exists, skipping download.
双赞!
恭喜!
我们已经从研究论文一路走到了在我们自定义图像上可用的模型代码!
主要收获¶
- 随着机器学习的爆发,每天都有新的研究论文详细介绍进展。要跟上所有这些是不可能的,但你可以将其缩小到自己的应用场景,比如我们在这里所做的,为FoodVision Mini复现一篇计算机视觉论文。
- 机器学习研究论文通常包含由聪明人组成的团队数月的研究成果,压缩在几页纸上(因此提取所有细节并完全复现论文可能有点挑战)。
- 复现论文的目标是将机器学习研究论文(文本和数学)转化为可用的代码。
- 尽管如此,许多机器学习研究团队开始在论文中发布代码,查看这一点的最佳地点之一是Paperswithcode.com
- 将机器学习研究论文分解为输入和输出(每个层/块/模型的输入和输出是什么?)和层(每个层如何处理输入?)以及块(层的集合),并逐步复现每个部分(就像我们在本笔记本中所做的那样),对于理解非常有帮助。
- 许多最先进的模型架构都有预训练模型,借助迁移学习的力量,这些模型通常在小数据上表现非常好。
- 较大的模型通常表现更好,但占用空间也更大(它们占用更多存储空间,推理时间可能更长)。
- 一个重要问题是:从部署角度来看,较大模型的额外性能是否值得/与应用场景相符?
练习¶
注意: 这些练习期望使用
torchvisionv0.13+(2022年7月发布),之前的版本可能也能工作,但可能会出现错误。
所有练习都专注于练习上述代码。
你应该能够通过参考每个部分或遵循所链接的资源来完成它们。
所有练习都应该使用设备无关代码完成。
资源:
- 第08讲的练习模板笔记本。
- 第08讲的示例解决方案笔记本(尝试练习之前查看这个)。
- 在YouTube上观看解决方案的视频讲解(包括所有错误)。
- 使用内置的PyTorch transformer层复制我们创建的ViT架构。
- 你需要研究如何用
torch.nn.TransformerEncoderLayer()替换我们的TransformerEncoderBlock()类(这些包含与我们自定义块相同的层)。 - 你可以通过
torch.nn.TransformerEncoder()将torch.nn.TransformerEncoderLayer()堆叠在一起。
- 你需要研究如何用
- 将我们创建的自定义ViT架构转换为Python脚本,例如,
vit.py。- 你应该能够通过类似
from vit import ViT的方式导入整个ViT模型。
- 你应该能够通过类似
- 在一个预训练的ViT特征提取器模型(就像我们在08. PyTorch论文复现第10节中制作的那个)上训练20%的披萨、牛排和寿司数据集(就像我们在07. PyTorch实验跟踪第7.3节中使用的数据集)。
- 看看它的性能与我们之前在08. PyTorch论文复现第10.6节中比较的EffNetB2模型相比如何。
- 尝试重复练习3的步骤,但这次使用
torchvision.models.vit_b_16()中的"ViT_B_16_Weights.IMAGENET1K_SWAG_E2E_V1"预训练权重。- 注意: 使用SWAG权重的ViT预训练模型有一个最小输入图像尺寸
(384, 384)(练习3中的预训练ViT的最小输入尺寸是(224, 224)),尽管这可以在权重的.transforms()方法中访问。
- 注意: 使用SWAG权重的ViT预训练模型有一个最小输入图像尺寸
- 我们的自定义ViT模型架构与ViT论文中的架构非常接近,然而,我们的训练方案缺少了一些东西。研究ViT论文表3中我们错过的一些主题,并为每个主题写一句话,说明它如何有助于训练:
- ImageNet-21k预训练(更多数据)。
- 学习率预热。
- 学习率衰减。
- 梯度裁剪。
课外拓展¶
- Vision Transformer自发布以来经历了多次迭代和调整,截至2022年7月,最简洁且性能最佳的版本可在《Better plain ViT baselines for ImageNet-1k》中查看。尽管有这些升级,本笔记本仍坚持复现一个“原始的Vision Transformer”,因为理解了原始结构,就能更好地过渡到不同迭代版本。
- lucidrains在GitHub上的
vit-pytorch仓库是PyTorch实现的各种ViT架构最全面的资源之一。这是一个极好的参考资料,我经常使用它来创建本章节的内容。 - PyTorch在GitHub上有自己的ViT架构实现,它是
torchvision.models中预训练ViT模型的基础。 - Jay Alammar在其博客上对注意力机制(Transformer模型的基础)和Transformer模型有精彩的插图和解释。
- Adrish Dey对层归一化(ViT架构的主要组成部分)的详细解读有助于神经网络训练。
- 自注意力(及多头自注意力)机制是ViT架构以及许多其他Transformer架构的核心,它最初在《Attention is all you need》论文中被引入。
- Yannic Kilcher的YouTube频道是视觉化论文解读的绝佳资源,你可以观看他对以下论文的视频解读:
- Attention is all you need(引入Transformer架构的论文)。
- An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale(引入ViT架构的论文)。
